MATHS-LYCEE
Exercice 1 (8 points)
Déterminer la limite de chaque fonction à l'endroit indiqué,
et préciser l'asymptote à la courbe représentative de $f$ s'il y a lieu.
- $f(x)=-x+3sin x$ en $+\infty$
Limite par comparaison
Soit $f$ et $g$ définie sur $I=]a;+\infty[$ telles que $f(x)\leq g(x)$ sur $I$.
Si $\displaystyle \lim_{x \rightarrow +\infty}f(x)=+\infty$ alors $\displaystyle \lim_{x \rightarrow +\infty}g(x)=+\infty$
Si $\displaystyle \lim_{x \rightarrow +\infty}g(x)=-\infty$ alors $\displaystyle \lim_{x \rightarrow +\infty}f(x)=-\infty$Il faut déterminer la limite de chaque terme de la somme donc de $-x$ puis de $3sin(x)$Pour tout réel $x$ on $-1\leq sinx(x)\leq 1$
donc $-3\leq 3sinx(x)\leq 3$
et $-x-3\leq -x+3sinx(x)\leq -x+3$
$\displaystyle \lim_{x \rightarrow +\infty}-x+3=-\infty$
et $f(x)\leq -x+3$
- $f(x)=\dfrac{x+5}{4x+1}$ en $+\infty$
Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes...Il faut factoriser $x$ au numérateur et au dénominateur$\displaystyle \lim_{x \rightarrow +\infty}x+5=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}x+4=+\infty$
donc la limite du quotient est indéterminée.
On cherche la limite en $+\infty$ donc on peut supposer $x>0$
$f(x)=\dfrac{x+5}{4x+1}$
$\phantom{f(x)}=\dfrac{x\left(1+\dfrac{5}{x}\right)}{x\left(4+\dfrac{1}{x}\right)}$
$\phantom{f(x)}=\dfrac{1+\dfrac{5}{x}}{4+\dfrac{1}{x}}$
$\displaystyle \lim_{x \rightarrow +\infty}1+\dfrac{5}{x}=1$
et $\displaystyle \lim_{x \rightarrow +\infty}1+\dfrac{4}{x}=1$
La courbe représentative de $f$ admet une asymptote d'équation $y=1$ (parallèle à l'axe des abscisses) en $+\infty$ - $f(x)=\sqrt{x+2}-\sqrt{x+3}$ en $+\infty$
On pourra montrer que pour tout réel $x>-2$ on a $\sqrt{x+2}-\sqrt{x+3}=\dfrac{-1}{\sqrt{x+2}+\sqrt{x+3}}$Il s'agit d'un cas d'indétermination $+\infty- (+\infty)$
Il faut multiplier par l'expression conjuguée de $\sqrt{x+2}-\sqrt{x+3}$ soit $\sqrt{x+2}+\sqrt{x+3}$$\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x+2}=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x+3}=+\infty$
donc la limite de la différence est indéterminée
Pour tout réel $x>-2$ on a:
$f(x)=\sqrt{x+2}-\sqrt{x+3}$
$\phantom{f(x)}=\dfrac{(\sqrt{x+2}-\sqrt{x+3})(\sqrt{x+2}+\sqrt{x+3})}{\sqrt{x+2}+\sqrt{x+3}}$
$\phantom{f(x)}=\dfrac{\sqrt{x+2}^2-\sqrt{x+3}^2}{\sqrt{x+2}+\sqrt{x+3}}$
$\phantom{f(x)}=\dfrac{(x+2)-(x+3)}{\sqrt{x+2}+\sqrt{x+3}}$
$\phantom{f(x)}=\dfrac{x+2-x-3}{\sqrt{x+2}+\sqrt{x+3}}$
$\phantom{f(x)}=\dfrac{-1}{\sqrt{x+2}+\sqrt{x+3}}$
$\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x+2}=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x+3}=+\infty$
donc par somme $\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x+2}=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x+2}+\sqrt{x+3}=+\infty$
La courbe représentative de $f$ admet l'axe des abscisses pour asymptote en $+\infty$.
Exercice 2 (5 points)
La fonction $f$ est définie sur $]0;+\infty[$ par $f(x)=\dfrac{e^x}{x^2}$ et on donne ci-dessous sa représentation graphique $C_f$ dans un repère orthogonal.
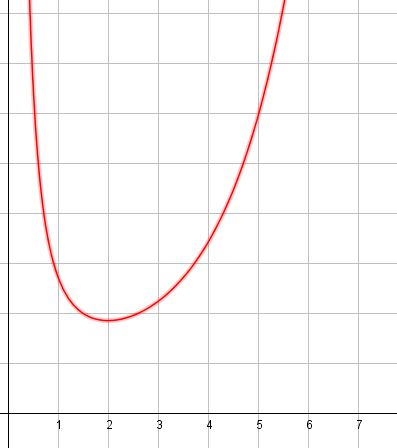
- A l'aide du graphique, conjecturer les limites de $f$ en $0$ et $+\infty$.
L'axe des ordonnées est une asymptote à la courbe.
- Démontrer les résultats ci-dessus.
Croissances comparées de $x^n$ et $e^x$
$n\in \mathbb{N}^*$
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{e^x}{x}=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{e^x}{x^n}=+\infty$Opérations sur les limites
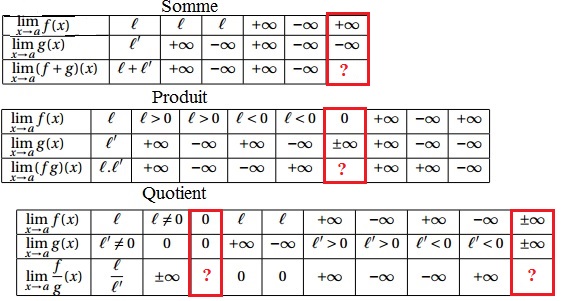rappel $e^0=1$$\displaystyle \lim_{x \rightarrow 0^+}e^x=1$ et $\displaystyle \lim_{x \rightarrow 0^+}x^2=0^+$
Exercice 3 (7 points)
Soit $f$ la fonction définie sur $]-2;+\infty[$ par $f(x)=\dfrac{x^2+4x+3}{x+2}$.
- Déterminer la limite de $f$ en $-2$.
Opérations sur les limites
Il faut chercher la limite du numérateur puir du dénominateur ainsi que son signe$\displaystyle \lim_{x \rightarrow -2^+}x^2+x+3=(-2)^2+4\times (-2)+3=4-8+3=-1$
et $\displaystyle \lim_{x \rightarrow -2^+}x+2=0^+$ car $x>2$ donc $x-2>0$
La droite d'équation $x=-2$ est asymptote à la courbe. - Déterminer la limite de $f$ en $+\infty$.
Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes...Il faut factoriser $x$ au numérateur et au dénominateur pour $x\neq 0$$\displaystyle \lim_{x \rightarrow +\infty}x^2+4x+3=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}x+2=+\infty$
donc la limite du quotient est indéterminée.
Pour tout réel $x>0$ (on cherche la limite en $+\infty$), on a:
$f(x)=\dfrac{x\left(x+4+\dfrac{3}{x}\right)}{x\left(1+\dfrac{2}{x}\right)}$
$~~~~~=\dfrac{x+4+\dfrac{3}{x}}{1+\dfrac{2}{x}}$
$\displaystyle \lim_{x \rightarrow +\infty}x+4=+\infty$ et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{3}{x}=0$
donc par somme $\displaystyle \lim_{x \rightarrow +\infty}x+4+\dfrac{3}{x}=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}1+\dfrac{2}{x}=1$
- La droite $(d)$ a pour équation $y=x+2$
- Montrer que $f(x)-(x+2)=\dfrac{-1}{x+2}$
$f(x)-(x+2)=\dfrac{x^2+4x+3}{x+2}-\dfrac{(x+2)(x+2)}{x+2}$
$\phantom{f(x)-(x+2)}=\dfrac{x^2+4x+3-(x^2+4x+4)}{x+2}$
$\phantom{f(x)-(x+2)}=\dfrac{x^2+4x+3-x^2-4x-4}{x+2}$
$\phantom{f(x)-(x+2)}=\dfrac{-1}{x+2}$ - En déduire $\displaystyle \lim_{x \rightarrow +\infty}f(x)-(x+2)$ et en donner une interprétation graphique.
$\displaystyle \lim_{x \rightarrow +\infty}x+2=+\infty$
Graphiquement $f(x)-(x+2)$ est "l'écart" entre la droite $(d)$ et $C_f$
et donc $(d)$ et $C_f$ sont infiniment proches quand $x\longrightarrow +\infty$
donc la droite $(d)$ est asymptote à la courbe en $+\infty$. - Déterminer la position relative de $(d)$ et $C_f$.
Il faut déterminer si $(d)$ est au-dessus ou en-dessous de $C_f$ en étudiant le signe de $f(x)-(x+2)$$f(x)-(x+2)=\dfrac{-1}{x+2}$
$x>-2$ donc $x+2>0$
donc $f(x)-(x+2)<0$
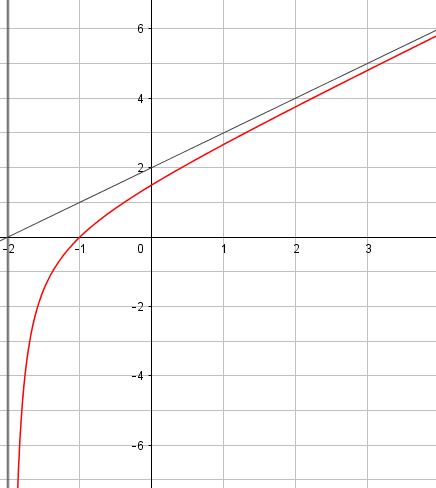
- Tracer les asymptotes à la courbe et compléter le tracé de $C_f$.
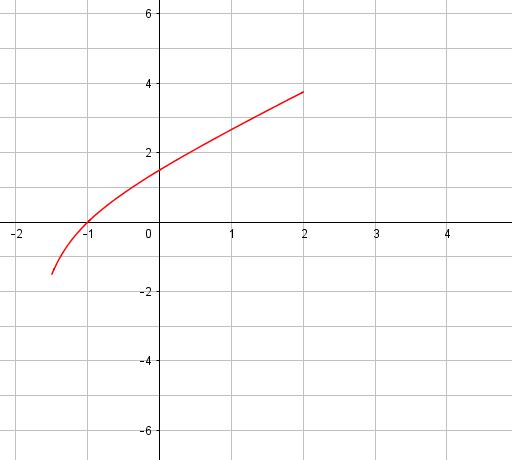Il faut tracer les droites d'équations $x=-2$ et $y=x+2$
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices. - Tracer les asymptotes à la courbe et compléter le tracé de $C_f$.
- Montrer que $f(x)-(x+2)=\dfrac{-1}{x+2}$