1. spécialité maths terminale
  2. chapitre
  3. devoir corrigé nº1087
PDF reservé aux abonnés
Exercice 1 (8 points)
L'objet de cet exercice est d'étudier la suite $\left(u_{n}\right)$ définie sur $\mathbb{N}$ par $u_{0} = 3$ et pour tout entier naturel $n$, $u_{n+1} = \dfrac{1}{2}\left(u_{n} + \dfrac{7}{u_{n}}\right)$.
On admettra que pour tout entier naturel $n$, $u_{n} > 0$.
  1. On désigne par $f$ la fonction définie sur l'intervalle $]0~;~+\infty[$ par $f(x) = \dfrac{1}{2}\left(x + \dfrac{7}{x}\right)$.
    Démontrer que la fonction $f$ admet un minimum.
    En déduire que pour tout entier naturel $n$, $u_{n} \geqslant \sqrt{7}$.

    Rappel de cours

    Angles associés

    Aide

    Il faut dresser le tableau de variation de $f$ en étudiant le signe de $f'(x)$

    Solution

    $f$ est la somme de fonctions dérivables sur $]0;+\infty[$
    donc est dérivable sur $]0;+\infty[$.
    $f'(x)=\dfrac{1}{2}\left(1- \dfrac{7}{x^2}\right)=\dfrac{1}{2}\left( \dfrac{x^2-7}{x^2}\right)$
    $x^2>0$ sur $]0;+\infty[$ donc $f'(x)$ est du signe de $x^2-7$
    Sur $]0;+\infty[$, $x^2-7=0$ s'annule pour $ x=\sqrt{7}$
    On a donc(sans les limites):

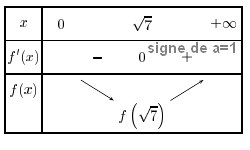
    donc le minimum de $f$ est $f\left(\sqrt{7}\right)$.
    $f(\sqrt{7}) = \dfrac{1}{2}\left(\sqrt{7}+ \dfrac{7}{\sqrt{7}}\right)$
    $\phantom{f(\sqrt{7})} = \dfrac{1}{2}\left( \sqrt{7}+ \dfrac{7\sqrt{7}}{\sqrt{7}\sqrt{7}}\right)$
    $\phantom{f(\sqrt{7})} = \dfrac{1}{2}\left( \sqrt{7}+ \sqrt{7}\right)$
    $\phantom{f(\sqrt{7})} = \sqrt{7}$
    On a $u_{n+1} = \dfrac{1}{2}\left(u_{n} + \dfrac{7}{u_{n}}\right)=f(u_n)$
    avec $f(u_n)\geq \sqrt{7}$
  2. Étudier les variations de la suite $(u_{n})$.

    Rappel de cours

    Étude des variations(différence de deux termes consécutifs)

    Pour étudier les variations de $(u_n)$, il faut comparer $u_{n+1}$ et $u_n$.
    Exprimer $u_{n+1}-u_n$ en fonction de $n$
    Étudier le signe de l'expression obtenue
    Si $u_{n+1}-u_n >0 $ alors$u_{n+1} >u_n$ et donc la suite $(u_n)$ est croissante.
    Si $u_{n+1}-u_n <0 $ alors$u_{n+1} < u_n$ et donc la suite $(u_n)$ est décroissante.

    Aide

    Il faut étudier le signe de $u_{n+1}-u_n$

    Solution

    $u_{n+1}-u_n=\dfrac{1}{2}\left(u_{n} + \dfrac{7}{u_{n}}\right)-u_n$
    $\phantom{u_{n+1}-u_n}=\dfrac{1}{2}\left( u_n+\dfrac{7}{u_{n}}-2u_n\right)$
    $\phantom{u_{n+1}-u_n}=\dfrac{1}{2}\left( \dfrac{7}{u_{n}}-u_n\right)$
    $\phantom{u_{n+1}-u_n}=\dfrac{1}{2}\left( \dfrac{7-u_n^2}{u_{n}}\right)$
    On admet que $u_n>0$ donc $u_{n+1}-u_n$ est du signe de $7-u_n^2$.
    or $u_n \geq \sqrt{7}$ donc $u_n^2\geq 7$ et $7-u_n^2\leq 0$
    donc $u_{n+1}-u_n\leq 0$
  3. La suite $\left(u_{n}\right)$ est-elle convergente ?

    Rappel de cours

    Suite majorée-suite minorée

    Une suite $(u_n)$ est majorée par $M$ si pour tout entier naturel $n$ on a $u_n\leq M$
    Une suite $(u_n)$ est minorée par $m$ si pour tout entier naturel $n$ on a $u_n\geq m$

    Une suite bornée est une suite à la fois minorée et majorée.

    Limite d'une suite majorée ou minorée

    Si la suite $(u_n)$ est croissante et majorée alors elle est convergente.
    Si la suite $(u_n)$ est décroissante et minorée alors elle est convergente

    Aide

    On utilise les questions 2 et 3

    Solution

    $(u_n)$ est décroissante et minorée par $\sqrt{7}$
  4. La limite $\ell$ de cette suite est telle que $\ell =f(\ell)$.
    En déduire $\displaystyle \lim_{n \rightarrow +\infty} u_n$.

    Solution

    On résout sur $[\sqrt{7};+\infty[$ puisque $u_n\geq \sqrt{7}$
    $f(\ell)=\ell \Longleftrightarrow \ell=\dfrac{1}{2}\left(\ell+\dfrac{7}{\ell}\right)$
    $\phantom{f(\ell)=\ell} \Longleftrightarrow 2\ell=\ell+\dfrac{7}{\ell}$
    $\phantom{f(\ell)=\ell} \Longleftrightarrow \ell=\dfrac{7}{\ell}$
    $\phantom{f(\ell)=\ell} \Longleftrightarrow \ell^2=7$
    $\phantom{f(\ell)=\ell} \Longleftrightarrow \ell=\sqrt{7}$ car $\ell>0$
Exercice 2 (12 points)
On considère les suites $(u_n)$ et $(v_n)$ définies sur $\mathbb{N}$ par :
$u_0=3$ et $u_{n+1}=\dfrac{u_n+v_n}{2}$ et $v_0=4$ et $v_{n+1}=\dfrac{u_{n+1} + v_n}{2}$.
  1. Calculer $u_1$, $v_1$, $u_2$ et $v_2$.

    Aide

    On prendr successivement $n=0$ puis $n=1$ dans les relations données.

    Solution

    En prenant $n=0$, on a:
    $u_{1}=\dfrac{u_0+v_0}{2}=\dfrac{3+4}{2}=\dfrac{7}{2}$
    et $v_{1}=\dfrac{u_{1} +v_0}{2}=\dfrac{\dfrac{7}{2}+4}{2}=\dfrac{\dfrac{15}{2}}{2}=\dfrac{15}{4}$.
    En prenant $n=1$ dans les relations données, on a:

    $u_{2}=\dfrac{u_1+v_1}{2}=\dfrac{\dfrac{7}{2}+\dfrac{15}{4}}{2}=\dfrac{\dfrac{29}{4}}{2}=\dfrac{29}{8}$
    et $v_{2}=\dfrac{u_{2} +v_1}{2}=\dfrac{\dfrac{29}{8}+\dfrac{15}{4}}{2}=\dfrac{\dfrac{59}{8}}{2}=\dfrac{59}{16}$.
  2. On considère l'algorithme ci-dessous.
    Compléter cet algorithme pour qu'il affiche les termes des suites $(u_n)$ et $(v_n)$ jusqu'à l'indice 20.

    Aide

    A chaque passage dans la boucle, on veut calculer les termes $u_{n+1}$ et $v_{n+1}$ en fonction de $U$ et $V$ correspondant aux termes $u_n$ et $v_n$.

    Solution

    Au premier passage dans la boucle POUR ($k=1$, on calcule donc $u_1$ connaissant $u_0=U=3$ et $v_0=V=4$ et $v_1$ avec $v_0=V$ et $u_1=U$ car $U$ a pris l valeur de $u_1$ à la ligne précédente (calcul de $U$.
    Il faut donc faire 20 passages dans la boucle POUR.
  3. L'algorithme ci-dessus affiche les valeurs suivantes(arrondies aux millièmes):

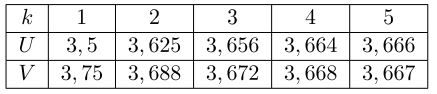
    Conjecturer les variations et limites des suite $(u_n)$ et $(v_n)$.

    Aide

    Rappel: conjecturer signifie constater (sans démontrer)

    Solution

    Il semble donc que la suite $(u_n)$ soit croissante et convergente (limite proche de 3,6) et que $(v_n)$ soit décroissante et que sa limite soit également proche de 3,6.
  4. . On définit les deux suites $(w_n)$ et $(t_n)$ sur $\mathbb{N}$ par $w_n= v_n- u_n $ et $t_n=\dfrac{u_n + 2v_n}{3}$.
    Montrer que $(w_n)$ est géométrique(on précisera sa raison et son premier terme) et que $(t_n)$ est constante.

    Rappel de cours

    Suite géométrique

    Une suite $(u_n)$ est géométrique s'il existe un réel $q$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n\times q$
    $q$ est la raison de la suite.
    Le quotient de deux termes consécutifs est égal à la raison soit $\dfrac{u_{n+1}}{u_n}=q$

    Aide

    Il faut montrer que $w_{n+1}=qw_n$ en utilisant $w_{n+1}=v_{n+1}-u_{n+1}$ et les relations définissant les suites $(u_n)$ et $(w_n)$.

    Solution

    On a $w_n=v_n-u_n$ donc $w_{n+1}=v_{n+1}-u_{n+1}$
    avec $u_{n+1}=\dfrac{u_n+v_n}{2}$ et $v_{n+1}=\dfrac{u_{n+1} +v_n}{2}$.
    $w_{n+1}=v_{n+1}-u_{n+1}$
    $\phantom{w_{n+1}}=\dfrac{u_{n+1} +v_n}{2}-\dfrac{u_n+v_n}{2}$
    $\phantom{w_{n+1}}=\dfrac{u_{n+1}-u_n}{2}$
    $\phantom{w_{n+1}}=\dfrac{\dfrac{u_n+v_n}{2}-u_n}{2}$
    $\phantom{w_{n+1}}=\dfrac{\dfrac{-u_n+v_n}{2}}{2}$
    $\phantom{w_{n+1}}=\dfrac{v_n-u_n}{4}$
    $\phantom{w_{n+1}}=\dfrac{w_n}{4}$
    donc $w_{n+1}=\dfrac{1}{4}w_n$ et $w_0=v_0-u_0=4-3=1$

    $t_n=\dfrac{u_n + 2v_n}{3}$ donc $t_{n+1}= \dfrac{u_{n+1} + 2v_{n+1}}{3}$
    $t_{n+1}=\dfrac{u_{n+1} + 2v_{n+1}}{3}$
    $\phantom{t_{n+1}}=\dfrac{\dfrac{u_n+v_n}{2}+ 2\dfrac{u_{n+1}+v_n}{2}}{3}$
    $\phantom{t_{n+1}}=\dfrac{\dfrac{u_n+v_n+2u_{n+1}+2v_n}{2}}{3}$
    $\phantom{t_{n+1}}=\dfrac{u_n+2u_{n+1}+3v_n}{6}$
    $\phantom{t_{n+1}}=\dfrac{u_n+2\dfrac{u_n+v_n}{2}+3v_n}{6}$
    $\phantom{t_{n+1}}=\dfrac{u_n+u_n+v_n+3v_n}{6}$
    $\phantom{t_{n+1}}=\dfrac{2u_n+4v_n}{6}$
    $\phantom{t_{n+1}}=\dfrac{2(u_n+2v_n)}{6}$
    $\phantom{t_{n+1}}=\dfrac{u_n+2v_n}{3}$
    $\phantom{t_{n+1}}=t_n$
  5. Exprimer $w_n$ en fonction de $n$ et calculer $t_n$ pour tout entier naturel $n$.

    Rappel de cours

    Forme explicite d'une suite géométrique

    Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
    $u_n=u_0\times q^n$
    et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$

    Aide

    $(w_n)$ est géométrique et $(t_n)$ est constante.

    Solution

    $(w_n)$ géométrique de raison $q=\dfrac{1}{4}$ et premier terme $w_0=1$ donc $w_n=w_0q^n=\dfrac{1}{4^n}$
    et $t_n=t_0=\dfrac{u_0+2v_0}{3}=\dfrac{11}{3}$ car $(t_n)$ est une suite constante.
  6. En déduire l'expression de $u_n$ et $v_n$ en fonction de $n$.

    Aide

    On a $w_n=v_n-u_n$ et $t_n=\dfrac{u_n+2v_n}{3}$ soit $3t_n=u_n+2v_n$
    On peut donc remplacer $v_n$ par $w_n+u_n$
    D'autre part on peut exprimer $w_n$ en fonction de $n$ et on a $t_n=t_0$ (à calculer)

    Solution

    On a $w_n=v_n-u_n$ donc $v_n= w_n+u_n$
    et $t_n=\dfrac{u_n+2v_n}{3}$ soit $3t_n=u_n+2v_n$
    donc $3t_n=u_n+2(w_n+u_n)$ (en remplaçant $v_n$ par $w_n+u_n$)
    $3t_n=u_n+2(w_n+u_n)\Longleftrightarrow 3t_n=u_n+2w_n+2u_n$
    $\phantom{3t_n=u_n+2(w_n+u_n)}\Longleftrightarrow 3t_n-2w_n=3u_n$
    $\phantom{3t_n=u_n+2(w_n+u_n)}\Longleftrightarrow u_n= t_n-\dfrac{2w_n}{3}$
    donc $u_n= t_n-\dfrac{2w_n}{3}=\dfrac{11}{3}-\dfrac{2}{3\times 4^n}$
    $v_n=w_n+u_n=\dfrac{1}{4^n}+\dfrac{11}{3}-\dfrac{2}{3\times 4^n}=\dfrac{11}{3}+\dfrac{1}{3\times 4^n}$
  7. En déduire la limite des suites $(u_n)$ et $(v_n)$.

    Rappel de cours

    Limite de $q^n$ (suite géométrique)

    Si $q > 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=+\infty$
    Si $-1 < q < 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=0$

    Aide

    $u_n=\dfrac{11}{3}-\dfrac{2}{3\times 4^n}=\dfrac{11}{3}-\dfrac{2}{3}w_n$
    Il faut donc chercher la limite de $(w_n)$

    Solution

    $u_n=\dfrac{11}{3}-\dfrac{2}{3\times 4^n}=\dfrac{11}{3}-\dfrac{2}{3}w_n$
    $(w_n)$ est une suite géométrique de raison $q=\dfrac{1}{4}$ avec $q\in]-1;1[$
    donc $\displaystyle \lim_{n \rightarrow +\infty}w_n=0$

    de même $v_n=\dfrac{11}{3}+\dfrac{1}{3\times 4^n}=\dfrac{11}{3}+\dfrac{1}{3}w_n$


    On a $w_n=v_n-u_n$ et $\displaystyle \lim_{n \rightarrow +\infty} w_n=0$
    donc $\displaystyle \lim_{n \rightarrow +\infty}v_n=\displaystyle \lim_{n \rightarrow +\infty}u_n$

exercices semblables


Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
réf 1051: Variations d'une suite en utilisant la fonction associée
| 5-7mn |
réf 1083: suites liées (BAC S Asie 2012)
| mn |
réf 1074: algorithme recherche d'un seuil
| 8-12mn |