---

Résoudre les inéquations ci-dessous dans $\mathbb{R}$ et donner l'ensemble de solution sous forme d'un intervalle:

1. $-3x+5 < 2$

   Rappel de cours

   Produit de facteurs nul

   ---

   Un produit de facteurs est nul si l'un des facteurs est nul.
   $a \times b=0 \Longleftrightarrow a=0$ ou $b=0$
   

   Solution

   $-3x+5 < 2 \Longleftrightarrow -3x < 2-5$
   $\phantom{(-3x+5 < 2} \Longleftrightarrow -3x < -3$
   $\phantom{(-3x+5 < 2} \Longleftrightarrow x > \dfrac{-3}{-3}$ l'inégalité change de sens en divisant par $-3$
   
   $\phantom{(-3x+5 < 2} \Longleftrightarrow x > 1$
   $S=]1;+\infty[ $
2. $\dfrac{2}{3}x-1 \geq \dfrac{1}{2}$

   Aide

   On peut écrire tous les membres avcec le même dénominateur pour éliminer les fractions

   Solution

   $\dfrac{2}{3}x-1 \geq \dfrac{1}{2} \Longleftrightarrow \dfrac{4}{6}x-\dfrac{6}{6} \geq \dfrac{3}{6}$
   $\phantom{\dfrac{2}{3}x-1 \geq \dfrac{1}{2}} \Longleftrightarrow 4x-6 \geq 3$
   $\phantom{\dfrac{2}{3}x-1 \geq \dfrac{1}{2}} \Longleftrightarrow 4x-6 \geq 3$
   $\phantom{\dfrac{2}{3}x-1 \geq \dfrac{1}{2}} \Longleftrightarrow 4x \geq 3+6$
   $\phantom{\dfrac{2}{3}x-1 \geq \dfrac{1}{2}} \Longleftrightarrow 4x \geq 9$
   $\phantom{\dfrac{2}{3}x-1 \geq \dfrac{1}{2}} \Longleftrightarrow x \geq \dfrac{9}{4}$
   $S=\left[\dfrac{9}{4};+\infty\right[$

$ABC$ sont trois points tels qu'une valeur approchée aux dixièmes de $AB$ est $5$cm et celle de $BC$ est $4$cm.

1. Donner un encadrement de $AB$ et de $BC$.

   Rappel de cours

   Valeur approchée d'un réel

   ---

   Si $x \in [a;b]$ alors le centre de l'intervalle $c=\dfrac{a+b}{2}$ est une valeur approchée de $x$ avec la précision $r=b-c=c-a$ (rayon de l'intervalle de centre $c$).
   Par exemple si $2,7$ est une valeur approchée de $x$ à $0,1$ près alors on a $2,7-0,1 < x < 2,7+0,1$ soit $2,6\leq x \leq 2,8$.

   Solution

   On a alors $5-0,1 \leq AB \leq 5+0,1$ et $4-0,1 \leq BC \leq 4+0,1$
   donc $4,9 \leq AB \leq 5,1$ et $3,9 \leq BC \leq 4,1$.
2. $ABCD$ est un rectangle, donner un encadrement et une valeur approchée du périmètre de ce rectangle.

   Rappel de cours

   Opérations sur les inégalités

   ---

   Soit $a$, $b$, $c$ et $d$ quatre réels.
   . $a\leq b \Longleftarrow a+c\leq b+c$
   On ne change pas une inégalité en ajoutant (ou soustrayant) un même nombre aux deux membres)
   - Si $a\leq c$ et $c\leq d$ alors $a+c\leq b+d$
   On peut ajouter membre à membre deux inégalités.
   - Si $c>0$, $a\leq b\Longleftrightarrow ac\leq bc$
   On ne change pas une inégalité en multipliant les deux membres par un même nombre strictement positif.
   - Si $c<0$, $a\leq b\Longleftrightarrow ac\geq bc$
   Une inégalité change de sens en multipliant les deux membres par un même nombre strictement négatif.

   Rappel de cours

   Déterminer le centre et le rayon d'un intervalle

   ---

   L'intervalle $I=[\alpha;\beta]$ avec $\alpha < \beta$. Le centre de $I$ est $a=\dfrac{\alpha+\beta}{2}$ (milieu du segment formé des points d'abscisses $\alpha$ et $\beta$)
   Le rayon est $r=\dfrac{|\beta-\alpha|}{2}=|\beta-a|$.
   On a alors $I=[a-r;a+r]$.

   Solution

   $P=2(AB+BC)$
   $4,9 \leq AB \leq 5,1$
   $3,9 \leq BC \leq 4,1$.
   donc $4,9+3,9 \leq AB+BC \leq 5,1+4,1$ (en ajoutant membre à membre)
   soit $8,8 \leq AB+BC \leq 9,2$
   donc $2\times 8,8 \leq 2(AB+BC) \leq 2\times 9,2$
   Le périmètre est compris entre $17,6$cm et $18,4$cm.
   $P$ appartient à l'intervalle $[17,6;18,4]$ de centre $c=\dfrac{17,6+18,4}{2}=18$ et de rayon $r=d(18,4;18)=|18,4-18|=0,4$
   donc une valeur approchée du périmètre est 18cm avec la précision $0,4$cm.
3. $ABCD$ est un rectangle, donner un encadrement et une valeur approchée de l'aire de ce rectangle.

   Aide

   On mutliplie les encadrements membre à membre

   Solution

   $A=AB\times BC$
   $4,9 \leq AB \leq 5,1$
   $3,9 \leq BC \leq 4,1$
   donc $4,9\times 3,9 \leq AB\times BC \leq 5,1\times 4,1$ (en multipliant membre à membre)
   soit $19,11 \leq AB\times BC \leq 20,91$
   
   L'aire est comprise entre $19,11$cm$^2$ et $20,91$cm$^2$.
   L'aire $A$ appartient à l'intervalle $[19,11;20,91]$ de centre $c=\dfrac{19,11+20,91}{2}=20,01$ et de rayon $r=d(20,91;20,01)=|20,91-20,01|=0,9$
   donc une valeur approchée de l'aire est $20,01$cm$^2$ avec la précision $0,9$cm$^2$.

On propose deux formules pour les voyages en métro:
- formule 1: un abonnement mensuel de 30 euros et ensuite $0,50$ euros par voyage
- formule 2: sans abonnement avec un prix de $1,40$ euros par voyage
On note $x$ le nombre de voyages mensuel (par mois) et $f(x$ et $g(x)$ la dépense respectivement avec les formules 1 et 2.

1. Exprimer $f(x)$ et $g(x)$ en fonction de $x$.

   Aide

   Si on fait $x$ voyages au prix de $p$ euros le voyage alors on dépense $x\times p$ euros.

   Solution

   $f(x)=30+0,5\times x=0,5x+30$
   $g(x)=x\times 1,4=1,4x$
   $f(x)=0,5x+30$ et $g(x)=1,4x$.
2. Résoudre $f(x) > 50$ et interpréter ce résultat dans le cadre du problème posé.

   Solution

   $f(x) > 50 \Longleftrightarrow 0,5x+30 > 50$
   $\phantom{f(x) > 50} \Longleftrightarrow 0,5x > 50-30$
   $\phantom{f(x) > 50} \Longleftrightarrow 0,5x > 20$
   $\phantom{f(x) > 50} \Longleftrightarrow x > \dfrac{20}{0,5}$
   $\phantom{f(x) > 50} \Longleftrightarrow x > 40$
   $f(x) > 50$ pour $x > 40$.
   Si on fait plus de 40 voyages dans le mois, on va payer plus de 50 euros avec la formule 1.
3. Résoudre $f(x) > g(x)$ et interpréter ce résultat dans le cadre du problème posé.

   Solution

   $f(x) > g(x) \Longleftrightarrow 0,5x+30 > 1,4x$
   $\phantom{f(x) > g(x)} \Longleftrightarrow 0,5x -1,4x > -30$
   $\phantom{f(x) > g(x)} \Longleftrightarrow -0,9x > -30$
   $\phantom{f(x) > g(x)} \Longleftrightarrow x < \dfrac{-30}{-0,9}$ l'inégalité change de sens en divisant par $-0,9$
   $\phantom{f(x) > g(x)} \Longleftrightarrow x < \dfrac{300}{9}$
   $\phantom{f(x) > g(x)} \Longleftrightarrow x < \dfrac{100}{3}$
   $S=\left[0; \dfrac{100}{3}\right[$
   $\dfrac{100}{3} \approx 33,33$ et $x$ est un entier (nombre de voyages)
   donc on doit avoir $x\leq 33$
   Le tarif 2 est plus avantageux si on fait moins de 33 voyages.
4. Représenter les deux fonctions dans le repère ci-dessous et contrôler graphiquement les solutions de la question précédente.
   

   Rappel de cours

   Fonction affine

   ---

   Une fonction afffine est définie sur $\mathbb{R}$ par $f(x)=ax+b$.
   La représentation graphique d'une fonction affine est une droite coupant l'axe des ordonnées au point $(0;b)$ et l'axe des abscisses au point $\left(\dfrac{-b}{a}\right)$ (si $a\neq 0$).
   Si $a=0$ alors la droite est parallèle à l'axe des abscisses.

   Solution

   $f$ est une fonction affine et $g$ une fonction linéaire donc les représentations graphiques de $f$ et $g$ sont des droites.
   $f(0)=30$ et $f(10)=0,5\times 10+30=35$ (en vert)
   $g(0)=0$ et $g(10)=1,4\times 10=14$ (en rouge)
   
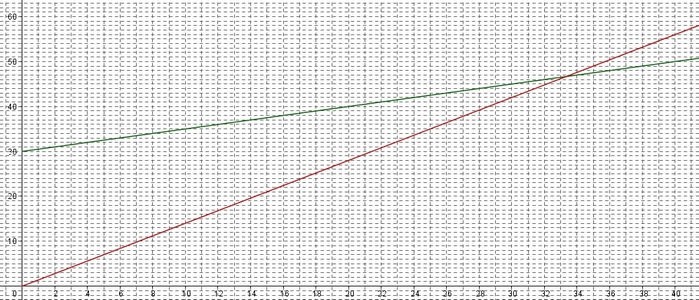
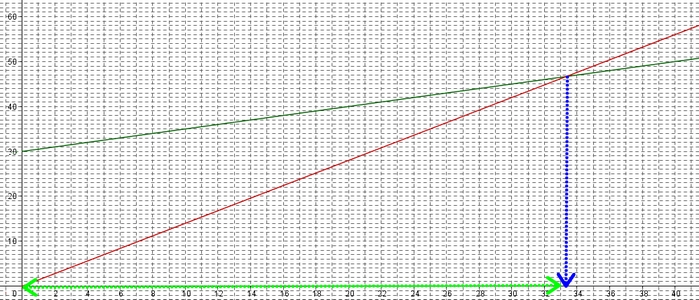
   On a donc bien $f(x)> g(x)$, c'est à dire la droite verte au-dessus de la rouge pour $x\leq 33$