Exercice 1 (5 points)
On joue au jeu de pile ou face avec une pièce parfaitement équilibrée.
- Quelle est la fréquence théorique d'apparition de la face pile ?
La fréquence théorique d'apparition de la face Pile est $\dfrac{1}{2}=0,5$.
- Au cours de 400 lancers, on a obtenu 235 fois la face pile.
Peut-on considérer que la pièce est équilibrée au seuil de 95\?Intervalle de fluctuation
On prélève un échantillon de taille $n$ dans une population.
On note $p$ la fréquence du caractère dans la population totale.
On note $f$ la fréquence du caractère dans l'échantillon prélevé.
Si $0,2\leq p\leq 0,80$et $n\geq 25$ alors dans au moins 95\ des cas,
$f$ appartient à l'intervalle $I_F=\left[p-\dfrac{1}{\sqrt{n}} ; p+\dfrac{1}{\sqrt{n}}\right]$ (intervalle de fluctuation de l'échantillon de taille $n$)Prise de décision
On veut finalement savoir si l'hypothèse formulée, à savoir la fréquence $p$ de la population totale, peut être validée ou non.
On utilise alors la fréquence $f$ de l'échantillon:
Si $f\in I_F$ alors on peut valider l'hypothèse $p$ au seuil de confiance de 95% Si $f\notin I_F$, on peut rejeter l'hypothèse $p$ avec un risque d'erreur maximum de 5%penser á vérifier que les conditions d'application pour effectuer les calculs sont satisfaitesOn ici $n\geq 25$ puisque $n=400$.
$p=0,5$ donc on a bien $p\in[0,2;0,8]$.
$p-\dfrac{1}{\sqrt{n}}=0,5-\dfrac{1}{\sqrt{400}}= 0,45$
$p+\dfrac{1}{\sqrt{n}}=0,5+\dfrac{1}{\sqrt{400}}= 0,55$
La fréquence observée sur l'échantillon des 400 lancers est $f=\dfrac{235}{400}=0,5875$
$f\notin I_F$
Exercice 2 (5 points)
Un candidat aux élection affirme qu'il va recueillir 54% des votes.
On effectue un sondage auprès de 350 personnes, et 182 déclarent avoir l'intention de voter pour ce candidat.
- Déterminer une intervalle de fluctuation au seuil de 95%. On arrondira à $10^{-3}$.
Intervalle de fluctuation
On prélève un échantillon de taille $n$ dans une population.
On note $p$ la fréquence du caractère dans la population totale.
On note $f$ la fréquence du caractère dans l'échantillon prélevé.
Si $0,2\leq p\leq 0,80$et $n\geq 25$ alors dans au moins 95\ des cas,
$f$ appartient à l'intervalle $I_F=\left[p-\dfrac{1}{\sqrt{n}} ; p+\dfrac{1}{\sqrt{n}}\right]$ (intervalle de fluctuation de l'échantillon de taille $n$)On a ici $p=0,54$ et $n=350$On ici $n\geq 25$ puisque $n=350$.
$p=\dfrac{54}{100}=0,54$ donc on a bien $p\in[0,2;0,8]$.
$p-\dfrac{1}{\sqrt{n}}=0,54-\dfrac{1}{\sqrt{35}0}\approx 0,486$ (on arrondi la borne inférieure par défaut)
$p+\dfrac{1}{\sqrt{n}}=0,54+\dfrac{1}{\sqrt{35}0}\approx 0,594$ (on arrondi la borne supérieure par excès)
- Compte tenu du résultat de ce sondage, doit-on remettre en cause l'affirmation de ce candidat?.
Prise de décision
On veut finalement savoir si l'hypothèse formulée, à savoir la fréquence $p$ de la population totale, peut être validée ou non.
On utilise alors la fréquence $f$ de l'échantillon:
Si $f\in I_F$ alors on peut valider l'hypothèse $p$ au seuil de confiance de 95% Si $f\notin I_F$, on peut rejeter l'hypothèse $p$ avec un risque d'erreur maximum de 5%On a ici $f=\dfrac{182}{350}=0,52$La fréquence observée sur l'échantillon est $f=\dfrac{182}{350}=0,52$
$f\in I_F$
Exercice 3 (10 points)
Deux grossistes produisent des bulbes de tulipes:
- le premier, des bulbes à fleurs rouges dont 90% donnent une fleur,
- le second, des bulbes à fleurs jaunes dont 80% donnent une fleur.
Un horticulteur achète 70% des bulbes qu'il cultive au premier grossiste et le reste au second. Un bulbe donne au plus une fleur. L'horticulteur plante un bulbe au hasard.
On utilisera le notations suivantes: $F$: "le bulbe donne une fleur" et $R$: "la fleur est rouge"
- Décrire l'événement $\overline F$ puis l'événement $\overline R$.
Notations des événements et probabilités
$\Omega$ est l'événement certain et $p(\Omega)=1$
$\oslash$ est l'événement impossible et $p(\oslash)=0$
$\overline{A}$ est l'événement contraire de A et est composé de toutes les issues de $\Omega$ qui ne sont pas contenue dans A et $p(\overline{A})=1-p(A)$$\overline F$ est l'événement contraire de $F$
donc $\overline F$ est l'événement "le bulbe ne donne pas de fleur"
et $\overline R$ est l'événement "le bulbe est un bulbe à fleur jaune" - Compléter le tableau à double entrée suivant en considérant par exemple un ensemble de 100 bulbes:
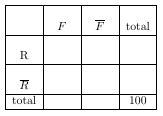 fboc.
fboc.
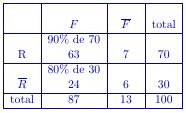
- En utilisant le tableau, déterminer la probabilité de:
- d'obtenir une fleur rouge ?
Il y a 63 fleurs rouges parmi les 100
donc $p(F\cap R)=\dfrac{63}{100}=0,63$
- d'obtenir une fleur jaune ?
Il y a 24 fleurs jaunes parmi les 100
donc $p(F\cap \overline{R})=\dfrac{24}{100}=0,24$
- de ne pas obtenir de fleur ?
Il y a au total 13 bulbes qui ne donnent pas de fleur
donc $p(\overline{F})=\dfrac{13}{100}=0,13$
- Le grossiste affirme que les bulbes qu'il vend donnent une fleur dans 80% des cas.
On effectue un test sur 400 bulbes et 305 donnent une fleur.
Doit-on remettre en cause l'affirmation du grossiste?0Intervalle de fluctuation
On prélève un échantillon de taille $n$ dans une population.
On note $p$ la fréquence du caractère dans la population totale.
On note $f$ la fréquence du caractère dans l'échantillon prélevé.
Si $0,2\leq p\leq 0,80$et $n\geq 25$ alors dans au moins 95\ des cas,
$f$ appartient à l'intervalle $I_F=\left[p-\dfrac{1}{\sqrt{n}} ; p+\dfrac{1}{\sqrt{n}}\right]$ (intervalle de fluctuation de l'échantillon de taille $n$)Prise de décision
On veut finalement savoir si l'hypothèse formulée, à savoir la fréquence $p$ de la population totale, peut être validée ou non.
On utilise alors la fréquence $f$ de l'échantillon:
Si $f\in I_F$ alors on peut valider l'hypothèse $p$ au seuil de confiance de 95% Si $f\notin I_F$, on peut rejeter l'hypothèse $p$ avec un risque d'erreur maximum de 5%0 penser á vérifier que les conditions d'application pour effectuer les calculs sont satisfaites
Il faut déterminer l'intervalle de fluctuation.On ici $n\geq 25$ puisque $n=400$.
$p=\dfrac{80}{100}=0,8$ donc on a bien $p\in[0,2;0,8]$.
$p-\dfrac{1}{\sqrt{n}}=0,8-\dfrac{1}{\sqrt{400}}=0,75$
$p+\dfrac{1}{\sqrt{n}}=0,8+\dfrac{1}{\sqrt{400}}=0,85$
La fréquence de l'échantillon est $f=\dfrac{305}{400}=0,7625$
$f\in I_F$
vidéos semblables
Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.réf 533: Calcul de probabilités avec un tableau à double entrée
| 4mn30smn |
réf 534: Échantillonnage-prise de décision
| 4mn50smn |
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices. - En utilisant le tableau, déterminer la probabilité de: