MATHS-LYCEE
Exercice 1 (7 points)
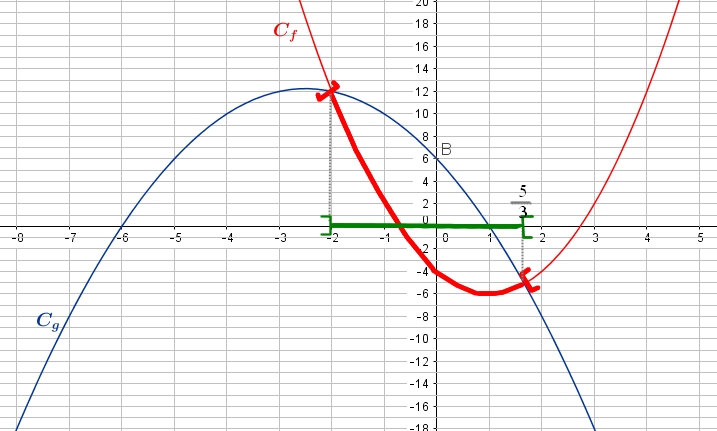
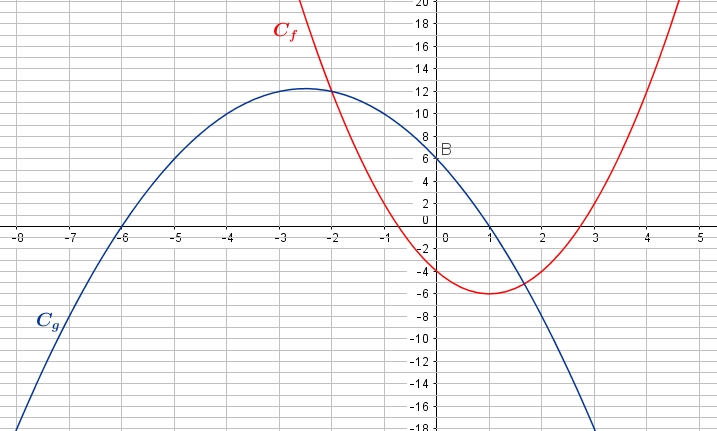
On considère les fonctions $f$ et $g$ définies sur $\mathbb{R}$ dont on donne les représentations graphiques $C_f$ et $C_g$ dans le repère ci-dessous.
- Déterminer à l'aide du graphique les coordonnées du sommet $S$ de la parabole $C_f$.
Le sommet de la parabole $C_f$ a pour coordonnées $(1;-6)$
- En déduire la forme canonique de $f$ en utilisant la question 1 et le point $A$ de la courbe $C_f$.
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$On a $f(x)=a(x-x_S)+y_S$ et $A(2;-4)$ donc $f(2)=-4$Le sommet de $C_f$ a pour coordonnées $(1;-6)$ et passe par le point de coordonnées $(2;-4)$ donc on va utiliser la forme canonique.
$f(x)=a(x-1)^2-6$ (on a $\alpha=1$ et $\beta=-6$)
Le point $A(2;-4)$ appartient à la courbe $C_f$ donc $f(2)=-4$.
$f(2)=-4 \Longleftrightarrow a(2-1)^2-6=-4 \Longleftrightarrow a=2$
- Déterminer graphiquement les solutions de l'équation $g(x)=0$
Graphiquement, les solutions de l'équation $g(x)=0$ sont les abscisses des points d'intersection de la courbe de de l'axe des abscisses.Graphiquement, les solutions de l'équation $g(x)=0$ sont les abscisses des points d'intersection de la courbe et de l'axe des abscisses
$C_g$ coupe l'axe des abscisses en $x_1=-6$ et $x_2=1$.
- En déduire la forme factorisée de $g$ en utilisant la question 3 et le point $B$ de la courbe $C_g$.
Forme factorisée
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$
alors la forme factorisée de $P$ est $P(x)=a(x-x_1)(x-x_2)$
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet une racine $x_1$
alors la forme factorisée de $P$ est $P(x)=a(x-x_1)^2$
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) n'admet aucune racine
alors la forme factorisée de $P$ n'existe pasOn a $g(x)=a(x-x_1)(x-x_2)$ et $B(0;6)$ appartient à la courbe $C_g$ donc $g(0)=6$$g(x)=0$ pour $x_1=-6$ et $x_2=1$ donc les racines de $g$ sont donc $x_1=-6$ et $x_2=1$
donc on va utiliser la forme factorisée de $g$
$g(x)=a(x-(-6))(x-1)=a(x+6)(x-1)$
$B(0;6)$ appartient à la courbe $C_g$ donc $g(0)=6$
$g(0)=6 \Longleftrightarrow a(0+6)(0-1)=6 \Longleftrightarrow a=-1$
- Donner la forme développée des fonctions $f$ et $g$.
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
$f(x)=2(x-1)^2-6=2(x^2-2x+1)-6=2x^2-4x-4$
$g(x)=-(x+6)(x-1)=-(x^2-x+6x-6)=-x^2+x-6x+6=-x^2-5x+6$
- Résoudre l'équation $2x^2-4x-4=-x^2-5x+6$
Comment peut-on contrôler les solutions obtenues sur le graphique?Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses. include126fcludSe ramener à une équation de la forme $ax^2+bx+c=0$ en "passant" tous les termes dans le membre de gauche$2x^2-4x-4=-x^2-5x+6 \Longleftrightarrow 2x^2-4x-4+x^2+5x-6=0$
$\phantom{2x^2-4x-4=-x^2-5x+6} \Longleftrightarrow 3x^2+x-10=0$
$x_1=-2$ est une solution car $3\times (-2)^2-2-10=0$
En utilisant le produit des deux racines:
$x_1x_2=\dfrac{c}{a}$ soit $-2x_2=\dfrac{-10}{3}$ donc $x_2=\dfrac{-10}{-6}=\dfrac{5}{3}$
On peut aussi calculer le discriminant $\Delta$ pour chercher les solutions de l'équation mais ce n'est pas indispensable ici.
Graphiquement, les solutions de l'équation $f(x)=g(x)$ sont les abscisses des points d'intersection des courbes $C_f$ et $C_g$.
Sur le graphique, $C_f$ et $C_g$ se coupent en $x_1=-2$ et $x_2=\dfrac{5}{3}\approx 1,6$ - En déduire, à l'aide du graphique, l'ensemble de solution de l'inéquation $f(x) < g(x)$.
Exercice 2 (7 points)
Résoudre:
- $-2x^2+5x-3>0$
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$
- Cas $\Delta=0$ (une racine $x_1$)
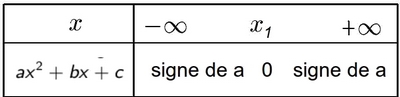
- Cas $\Delta<0$ (aucune racine)
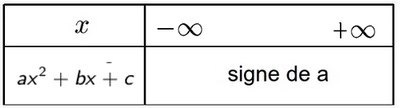Chercher les racines de $-2x^2+5x-3$.
Dresser le tableau de signes de $-2x^2+5x-3$.
Ecrire l'ensemble de solution.Racines de $-2x^2+5x-3$:
$-2+5-3=0$ donc $x_1=1$ est une racine de $-2x^2+5x-3$
$x_1x_2=\dfrac{c}{a}$ donc $1x_2=\dfrac{-3}{-2}=\dfrac{3}{2}$
On peut calculer le discriminant $\Delta$ mais ce n'est pas indispensable ici.
$\Delta=b^2-4ac=$ $\Delta>0$.......
Signe de $-2x^2+5x-3$:
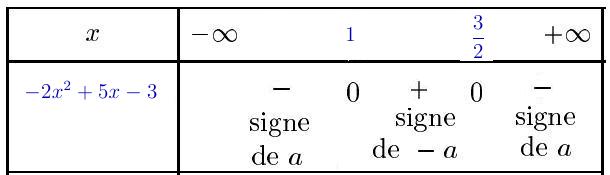
- $\dfrac{2x^2-5x+2}{x-3}\geq 0$
Chercher avant tout la valeur interdite
Déterminer les racines de $2x^2-5x+2$
Construire un tableau de signes avec le numérateur $2x^2-5x+2$ et le dénominateur $x-3$
ne pas oublier la double barreIl faut $x-3\neq 0$ soit $x\neq 3$
On résout cette inéquation sur $\mathbb{R} \setminus \lbrace -3 \rbrace$.
Racines de $2x^2-5x+2$:
$\Delta=b^2-4ac=(-5)^2-4\times 2\times 2=25-16=9$
$\Delta>0$ donc il y a deux racines:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-3}{4}=\dfrac{1}{2}$ et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+3}{4}=2$
Signe de $\dfrac{2x^2-5x+2}{x-3}$:
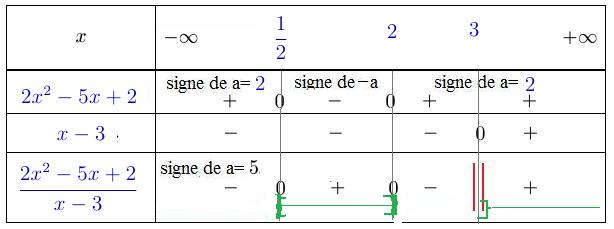
Exercice 3 (3 points)
Soit $P$ le polynôme défini sur $\mathbb{R}$ par : $P(x)=2x^3-3x^2+3x-10$.
- Montrer que pour tout réel $x$, on a $P(x)=(x-2)(2x^2+x+5)$.
0 Développer l'expression $(x-2)(2x^2+x+5)$ et vérifier que cela est égal à $P(x)$$(x-2)(2x^2+x+5)=2x^3+x^2+5x-4x^2-2x-10=2x^3-3x^2+3x-10=P(x)$
Ne pas écrire dès le départ que $P(x)=(x-2)(2x^2+x+5)=.....$
En effet, on veut vérifier que $P(x)=(x-2)(2x^2+x+5)$ donc on effectue le calcul en développant $(x-2)(2x^2+x+5)$ pour être certain que l'on obtient bien $P(x)$. - En déduire les solutions de l'équation $P(x)=0$.
Exercice 4 (4 points)
Une entreprise produit entre 2 et 50 appareils électroménagers par heure. Le coût horaire de production de $x$ appareils, en euros, est donné par:$C(x)=x^2+50x+76$, pour $2\leqslant x\leqslant 50$.
Le prix de vente unitaire d'un appareil est de 90 euros.
On suppose que tout appareil produit est vendu.
- Exprimer en fonction de $x$ la recette totale.
- En déduire que le bénéfice horaire réalisé par la fabrication et vente de ces $x$ appareils est donné par la fonction $B$ définie par $B(x)=-x^2+40x-76$.
- Dresser le tableau de variation de la fonction $B$ et en déduire le nombre d'appareils à produire pour que le bénéfice horaire soit maximum.
4
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$
- Cas $\Delta=0$ (une racine $x_1$)
- Cas $\Delta<0$ (aucune racine)
Chercher les coordonnées du sommet de la parabole représentatnt la fonction bénéfice.$\alpha=\dfrac{-40}{-2}=20$
$\beta=B(\alpha)=B(20)=-20^2+40\times 20-76=324$
Le coefficient $a$ de $x^2$ est $-1$ donc on a:
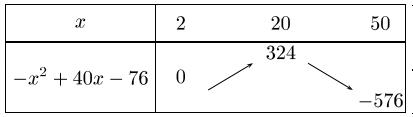
Le maximum de $B$ est atteint pour $x=20$.
- Dresser le tableau de signes de $-x^2+40x-76$.
On donne les racines $x_1=2$ et $x_2=38$ de $-x^2+40x-76$.
L'entreprise réalise-t-elle toujours des bénéfices? Justifier.
Fiche méthode
Si ce devoir vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Résolution d'équation commentées pas à pas
- exemples types d'équations pas à pas
infos: | 8-12mn |
vidéos semblables
Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.