1. spécialité maths première
  2. chapitre
  3. devoir corrigé nº893
PDF reservé aux abonnés
Exercice 1 (5 points)
Pour chaque question, une seule réponse est exacte parmi celles qui sont proposées.
Une réponse correcte rapporte 1 point, l'absence de réponse n'ajoute et n'enlève aucun point et une réponse fausse enlève 0,5 point.
Si le total des points de l'exercice est négatif, la note de l'exercice est ramenée à 0.
Recopier sur la copie la réponse correcte (rien ne doit être écrit sur le polycopié).
On ne demande aucune justification.
  1. Dans un repère orthonormé, on donne $\overrightarrow{u}(2;5)$ et $\overrightarrow{v}(-10;4)$.
    $\overrightarrow{u}$ et $\overrightarrow{v}$ sont
    colinéaires$~~~~~~~~$orthogonaux$~~~~~~~~~~$ aucune réponse ne convient

    Rappel de cours

    Produit scalaire dans un repère orthonormé

    Dans un repère orthonormé, si $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ on a:
    $\overrightarrow{u}.\overrightarrow{v}=xx'+yy'$

    Solution

    $\overrightarrow{u}.\overrightarrow{v}=2\times (-10)+5\times 4=-20+20=0$
  2. ABC est un triangle isocèle en A tel que AB=8, l'unité étant le cm, $\overrightarrow{AB}.\overrightarrow{AC}=$
    $64~~~~~~~~à-32~~~~~~32~~~~~~~~$ aucune réponse ne convient

    Solution

    $ABC$ est isocèle en A
    Pour calculer $\overrightarrow{AB}.\overrightarrow{AC}$ il faut connaître soit la longueur des trois côtés, soit la mesure de $\widehat{BAC}$, soit la position du projeté orthogonal de $C$ sur $(AB)$.
    Ici, on ne peut déterminer aucune de ces trois données
  3. ABCD est un rectangle tel que $AB=6$ et $AD=4$, l'unité étant le cm, $\overrightarrow{AB}.\overrightarrow{CA}=$
    $36~~~~~~~~-36~~~~~~~~-24~~~~~~~~$ aucune réponse ne convient

    Rappel de cours

    Produit scalaire et projeté orthogonal

    Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
    Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
    $\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
    et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)

    Aide

    On peut écrire $-\overrightarrow{AB}.\overrightarrow{AC}= \overrightarrow{AB}.\overrightarrow{CA}$
    On peut utilser le projeté orthogonal de $C$ sur $AB$.

    Solution

    $\overrightarrow{CA}= -\overrightarrow{AC}$
    donc $\overrightarrow{AB}.\overrightarrow{CA}= -\overrightarrow{AB}.\overrightarrow{AC}$
    $ABCD$ est un rectangle donc le projeté orthogonal de $C$ sur $(AB)$ est $B$ et l'angle $\widehat{BAC}$ est aigu
    donc $\overrightarrow{AB}.\overrightarrow{AC}=AB\times AB=AB^2$
    et donc $\overrightarrow{AB}.\overrightarrow{CA}= -\overrightarrow{AB}.\overrightarrow{AC}=-AB^2=-36$
  4. $A$ et $B$ sont deux points du plan tels que $AB=1$.
    L'ensemble des points M du plan vérifiant $\overrightarrow{AM}.\overrightarrow{AB}=\dfrac{1}{2}$ est
    la droite perpendiculaire à $(AB)$ passant par B
    la droite perpendiculaire à $(AB)$ passant par A
    la médiatrice de $[AB]~~~~~~$
    aucune des réponse ne convient

    Aide

    On peut utiliser le projeté orthogonal de $M$ sur $(AB)$
    ou bien utiliser un repère orthonormé dont $\overrightarrow{AB}$ est le vecteur unitaire sur l'axe des abscisses.

    Solution

    Soit $H$ le projeté orthogonal de $M$ sur $(AB)$.
    $\overrightarrow{AM}.\overrightarrow{AB}$ est positif et donc $H \in [AB)$.
    On a alors $\overrightarrow{AM}.\overrightarrow{AB}=AB\times AH$
    $AB\times AH =\dfrac{1}{2}$ donc $AH=\dfrac{1}{2AB}=\dfrac{1}{2}$ car $AB=1$.
    $AH=\dfrac{1}{2}$ et $H\in [AB)$ donc $H$ est le milieu de $[AB]$.
    L'ensemble des points $M$ du plan tels que $\overrightarrow{AM}.\overrightarrow{AB}=\dfrac{1}{2}$ est donc la droite perpendiculaire à $(AB)$ passant par $H$.
Exercice 2 (4 points)
On considère les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ orthogonaux tels que $||\overrightarrow{u}||=3$ et $||\overrightarrow{v}||=5$.
Calculer $(2\overrightarrow{u}+\overrightarrow{v}).(\overrightarrow{u}-2\overrightarrow{v})$

Rappel de cours

Propriétés du produit scalaire

Soient $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ trois vecteurs et $k$ un réel:
$\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}$
$(k \overrightarrow{u}).\overrightarrow{v}=k(\overrightarrow{u}.\overrightarrow{v})$

$(\overrightarrow{u}+\overrightarrow{v}).\overrightarrow{w}=\overrightarrow{u}.\overrightarrow{w}+\overrightarrow{v}.\overrightarrow{w}$

Orthogonalité

Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non nuls, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.

Aide

Développer l'expression et utiliser l'orthogonalité des deux vecteurs

Solution

$\overrightarrow{u}$ et $\overrightarrow{v}$ orthogonaux donc $\overrightarrow{u}.\overrightarrow{v}=0$
$(2\overrightarrow{u}+\overrightarrow{v}).(\overrightarrow{u}-2\overrightarrow{v})=2\overrightarrow{u}^2-4\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{v}.\overrightarrow{u}-2\overrightarrow{v}^2$
$\phantom{(2\overrightarrow{u}+\overrightarrow{v}).(\overrightarrow{u}-2\overrightarrow{v})}=2||u||^2-4\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{v}.\overrightarrow{u}-2||v||^2$
$\phantom{(2\overrightarrow{u}+\overrightarrow{v}).(\overrightarrow{u}-2\overrightarrow{v})}=18-2\times 25$
$\phantom{(2\overrightarrow{u}+\overrightarrow{v}).(\overrightarrow{u}-2\overrightarrow{v})}=-32$
Exercice 3 (6 points)
Soient deux points $A$ et $B$ avec $AB=6$.
  1. Déterminer l'ensemble $\mathcal{D}$ des points $M$ du plan tels que : $\overrightarrow{AM}.\overrightarrow{AB}=-12$ puis représenter cet ensemble.

    Rappel de cours

    Produit scalaire et projeté orthogonal

    Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
    Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
    $\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
    et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)

    Aide

    Il faut déterminer la position de $H$ projeté orthogonal de $M$ sur $(AB)$.

    Solution

    Soit $H$ le projeté orthogonal de $M$ sur $(AB)$.
    $\overrightarrow{AM}.\overrightarrow{AB}$ est négatif et donc $H \notin [AB)$ et donc $\widehat{BAM}$ est obtus.
    On a alors $\overrightarrow{AM}.\overrightarrow{AB}=-AB\times AH$
    $-AB\times AH =-12$ donc $AH=\dfrac{12}{AB}=\dfrac{12}{6}=2$ car $AB=6$.
    $AH=2$ et $H\notin [AB)$




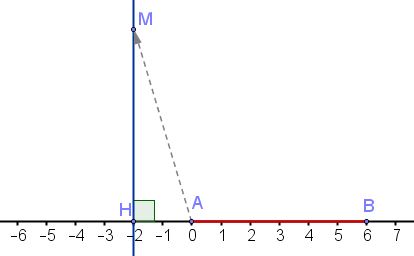
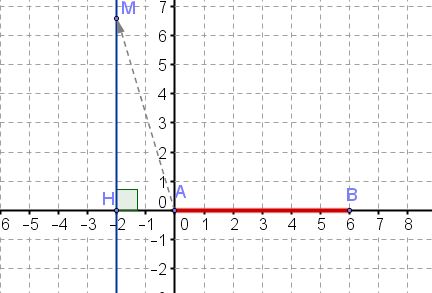
    En utilisant un repère orthonormé, en prenant $A$ pour origine et $(AB)$ pour axe des abscisses, on a $A(0;0)$ et $B(6;0)$.
    $\overrightarrow{AB}(6;0)$ et $\overrightarrow{AM}(x;y)$.
    $\overrightarrow{AM}.\overrightarrow{AB}=-12 \Longleftrightarrow 6x+0y=-12 \Longleftrightarrow x=-2$
    L'ensemble des points $M$ du plan tels que $\overrightarrow{AM}.\overrightarrow{AB}=-12$ est donc la droite d'équation $x=-2$.
  2. On note $I$ le milieu de $[AB]$.
    En décomposant $\overrightarrow{MA}=\overrightarrow{MI}+\overrightarrow{IA}$ et $\overrightarrow{MB}=\overrightarrow{MI}+\overrightarrow{IB}$, montrer que $\overrightarrow{MA}.\overrightarrow{MB}=16 \Longleftrightarrow MI^2=25$
    et en déduire l'ensemble des points $M$ tels que $\overrightarrow{MA}.\overrightarrow{MB}=16$.

    Rappel de cours

    Propriétés du produit scalaire

    Soient $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ trois vecteurs et $k$ un réel:
    $\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}$
    $(k \overrightarrow{u}).\overrightarrow{v}=k(\overrightarrow{u}.\overrightarrow{v})$

    $(\overrightarrow{u}+\overrightarrow{v}).\overrightarrow{w}=\overrightarrow{u}.\overrightarrow{w}+\overrightarrow{v}.\overrightarrow{w}$

    Aide

    On peut développer $(\overrightarrow{MI}+\overrightarrow{IA})(\overrightarrow{MI}+\overrightarrow{IB})$ et on a $\overrightarrow{AI}+\overrightarrow{BI}=\overrightarrow{0}$

    Solution

    On pose $I$ milieu de $[AB]$ et on a $\overrightarrow{AI}=-\overrightarrow{BI}$ ou bien encore $\overrightarrow{AI}+\overrightarrow{BI}=\overrightarrow{0}$
    $\overrightarrow{MA}.\overrightarrow{MB}=16 \Longleftrightarrow (\overrightarrow{MI}+\overrightarrow{IA})(\overrightarrow{MI}+\overrightarrow{IB})=16$
    $\phantom{\overrightarrow{MA}.\overrightarrow{MB}=16} \Longleftrightarrow MI^2+\overrightarrow{MI}.\overrightarrow{IA}+\overrightarrow{MI}.\overrightarrow{IB}+\overrightarrow{IA}.\overrightarrow{IB}=16$
    $\phantom{\overrightarrow{MA}.\overrightarrow{MB}=16} \Longleftrightarrow MI^2+\overrightarrow{MI}.(\overrightarrow{IA}+\overrightarrow{IB})-\overrightarrow{IA}.\overrightarrow{IA}=16$
    $\phantom{\overrightarrow{MA}.\overrightarrow{MB}=16} \Longleftrightarrow MI^2+\overrightarrow{MI}.\overrightarrow{0}-\overrightarrow{IA}^2=16$
    $\phantom{\overrightarrow{MA}.\overrightarrow{MB}=16} \Longleftrightarrow MI^2=IA^2+16$
    $\phantom{\overrightarrow{MA}.\overrightarrow{MB}=16} \Longleftrightarrow MI^2=25$
    $\phantom{\overrightarrow{MA}.\overrightarrow{MB}=16} \Longleftrightarrow MI=5$
Exercice 4 (5 points)
Problème ouvert: toute trace de recherche même incomplète sera prise en compte dans la notation.
On considère un rectangle $ABCD$ tel que $AB=2AD=12$ cm et les points $I$ et $J$ milieux respectifs de $[BC]$ et $[CD]$.
Déterminer la mesure de l'angle entre les droites $(AI)$ et $(AJ)$.

Aide

La méthode la plus simple est d'utiliser un repère orthonormé.

Solution

Si on utilise le repère orthonormé $(A;\overrightarrow{i};\overrightarrow{j})$ (voir figure), l'unité étant le cm.

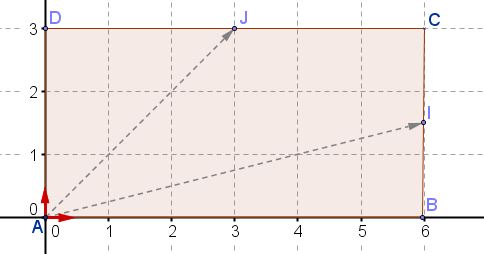
On a alors $I(12;3)$ et $J(6;6)$ et $\overrightarrow{AI}(12;3)$ et $\overrightarrow{AJ}(6;6)$.
$\overrightarrow{AI}.\overrightarrow{AJ}=12\times 6+3\times 6=90$
$||\overrightarrow{AI}||=AI=\sqrt{12^2+3^2}=\sqrt{144+9}=\sqrt{153}$
$||\overrightarrow{AJ}||=AJ=\sqrt{6^2+6^2}=\sqrt{36+36}=\sqrt{72}$
$\overrightarrow{AI}.\overrightarrow{AJ}=AI\times AJ\times cos(\overrightarrow{AI},\overrightarrow{AI})=\sqrt{153}\sqrt{72} cos(\overrightarrow{AI},\overrightarrow{AI})$
donc $\sqrt{153}\sqrt{72} cos(\overrightarrow{AI},\overrightarrow{AI})=90$
soit $cos(\overrightarrow{AI},\overrightarrow{AI})=\dfrac{90}{\sqrt{153}\sqrt{72} }$
et $cos^{-1}\left(\dfrac{90}{\sqrt{153}\sqrt{72} }\right)\approx 31^{\text{o}}$

On peut aussi calculer le produit scalaire $\overrightarrow{AI}.\overrightarrow{AJ}$ en utilisant les longueurs des segments $[AI]$, $[AJ]$ et $[IJ]$ avec $\overrightarrow{AI}.\overrightarrow{AJ}=\dfrac{AI^2+AJ^2-IJ^2}{2}$
On peut aussi calculer les mesures des angles $\widehat{DAJ}$ et $\widehat{IAB}$ en utilisant les triangles rectangles AJD et AIB.

vidéos semblables


Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.
réf 902: Choisir la bonne expression du produit scalaire
| 3mnmn |

exercices semblables


Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
réf 869: Produit scalaire et projeté orthogonal
| 4-6mn |
réf 870: Utiliser la définition du produit scalaire
| mn |
réf 874: Choisir la bonne expression
| 4-6mn |
réf 885: Calcul d'un angle dans un triangle avecun repère
| 6-10mn |