1. spécialité maths première
  2. chapitre
  3. devoir corrigé nº894
PDF reservé aux abonnés
Exercice 1 (5 points)
  1. $ABC$ est un triangle tel que $AB=6$cm, $AC=4$cm et $BC=7$cm.
    a. $64~~~~$ b. $-32~~~~$ c. $32~~~~$ d. aucune réponse ne convient

    Rappel de cours

    Produit scalaire avec les normes

    Pour tous vecteurs $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$ on a:
    $\overrightarrow{u}.\overrightarrow{v}=\dfrac{\mid \mid \overrightarrow{u}\mid \mid^2+\mid \mid \overrightarrow{v}\mid \mid^2-\mid \mid \overrightarrow{u}-\overrightarrow{v}\mid \mid^2}{2}$
    Dans le triangle $ABC$: $\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$

    Solution

    $\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC} }=\dfrac{6^2+4^2-7^2}{2}$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC} }=\dfrac{3}{2}$
  2. $A(2;4)$, $B(-1;3)$ et $C(1;-2)$ dans un repère orthonormé.
    $\overrightarrow{AB}.\overrightarrow{AC}=$
    a. $-3~~~~~~$ b. $9~~~~~~$ c. $-9~~~~~~~~$ d. aucune réponse ne convient

    Rappel de cours

    Produit scalaire dans un repère orthonormé

    Dans un repère orthonormé, si $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ on a:
    $\overrightarrow{u}.\overrightarrow{v}=xx'+yy'$

    Solution

    $\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=-1-2=-3\\ y_{\overrightarrow{AB}}=y_B-y_A=3-4=-1 \end{cases}$
    donc $\overrightarrow{AB}(-3;-1)$
    $\begin{cases} x_{\overrightarrow{AC}}=x_C-x_A=-1-2=-1 \\ y_{\overrightarrow{AC}}=y_C-y_A=-2-4=-6 \end{cases}$
    donc $\overrightarrow{AC}(-1;-6)$
    $\overrightarrow{AB}.\overrightarrow{AC}=x_{\overrightarrow{AB}}x_{\overrightarrow{AC}}+y_{\overrightarrow{AB}}y_{\overrightarrow{AC}}$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=(-3)\times (-1)+(-1)\times (-6)$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=9$
  3. $AB=6$cm, $AC=5$cm et $\widehat{BAC}=\dfrac{2\pi}{3}$ radians.
    $\overrightarrow{AB}.\overrightarrow{AC}=$
    a. $-15~~~~~~~$ b. $15~~~~~~~~$ c. $15\sqrt{3}~~~~~~~$ d. aucune réponse ne convient

    Rappel de cours

    Produit scalaire (définition)

    $\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
    $\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$

    Solution

    $\overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos(\widehat{BAC})$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=6\times 5\times cos(\dfrac{2\pi}{3})$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=30\times (\dfrac{-1}{2})$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=-15$
  4. $AB=6cm$ et $ABC$ est un triangle rectangle en $B$.
    $\overrightarrow{AB}.\overrightarrow{AC}=$
    a. $6~~~~~~~$ b. $12~~~~~~~~$ c. $36~~~~~~~$ d. aucune réponse ne convient

    Rappel de cours

    Produit scalaire et projeté orthogonal

    Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
    Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
    $\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
    et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)

    Solution

    $ABC$ est rectangle en $B$ donc le projeté orthogonal de $C$ sur $(AB)$ est le point $B$
    et $\widehat{BAC}$ est un angle aigu
    $\overrightarrow{AB}.\overrightarrow{AC}=AB\times AB$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=AB^2$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=36$
  5. $||\overrightarrow{u}||=||\overrightarrow{v}||=6$ et $\overrightarrow{u}.\overrightarrow{v}=-2$
    $\overrightarrow{u}.(\overrightarrow{u}-\overrightarrow{v})=$
    a. $34~~~~~~~$ b. $36~~~~~~~~$ c. $38~~~~~~~$ d. aucune réponse ne convient

    Rappel de cours

    Propriétés du produit scalaire

    Soient $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ trois vecteurs et $k$ un réel:
    $\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}$
    $(k \overrightarrow{u}).\overrightarrow{v}=k(\overrightarrow{u}.\overrightarrow{v})$

    $(\overrightarrow{u}+\overrightarrow{v}).\overrightarrow{w}=\overrightarrow{u}.\overrightarrow{w}+\overrightarrow{v}.\overrightarrow{w}$

    Solution

    $\overrightarrow{u}.(\overrightarrow{u}-\overrightarrow{v})$
    $=\overrightarrow{u}^2-\overrightarrow{u}.\overrightarrow{v}$
    $=6^2-(-2)$
    $=38$
Exercice 2 (5 points)
Dans le plan muni d'un repère orthonormé (unité le cm), on donne $A(2;1)$, $B(-1;-3)$ et $C(-3;0)$.
  1. Faire une figure.
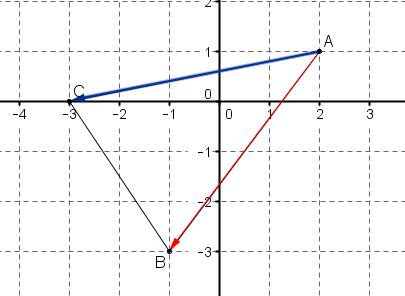
  2. Calculer $\overrightarrow{AB}.\overrightarrow{AC}$.

    Rappel de cours

    Coordonnées d'un vecteur défini par deux points

    Si $A(x_A;y_A)$ et $B(x_B;y_B)$ alors $\overrightarrow{AB}(x_B-x_A;y_B-y_A)$ (coordonnées du second point $-$ coordonnées du premier point)

    Produit scalaire dans un repère orthonormé

    Dans un repère orthonormé, si $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ on a:
    $\overrightarrow{u}.\overrightarrow{v}=xx'+yy'$

    Solution

    $\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=-1-2=-3\\ y_{\overrightarrow{AB}}=y_B-y_A=-3-1=-4 \end{cases}$
    donc $\overrightarrow{AB}(-3;-4)$
    $\begin{cases} x_{\overrightarrow{AC}}=x_C-x_A=-3-2=-5 \\ y_{\overrightarrow{AC}}=y_C-y_A=-0-1=-1 \end{cases}$
    donc $\overrightarrow{AC}(-5;-1)$
    $\overrightarrow{AB}.\overrightarrow{AC}=x_{\overrightarrow{AB}}x_{\overrightarrow{AC}}+y_{\overrightarrow{AB}}y_{\overrightarrow{AC}}$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=(-3)\times (-5)+(-4)\times (-1)$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=19$
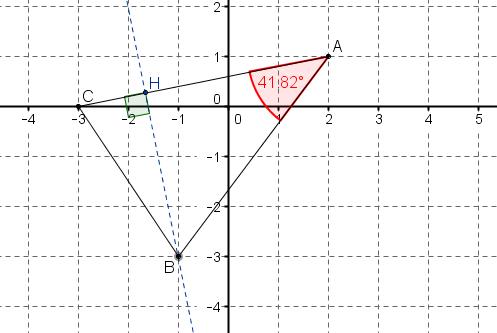
  3. Déterminer la mesure arrondie au dixième de degré de l'angle $\widehat{BAC}$.

    Rappel de cours

    Distance dans un repère

    Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
    $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
    Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$

    Produit scalaire (définition)

    $\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
    $\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$

    Aide

    Calculer $AB$ et $AC $ puis écrire une équation d'inconnue $cos(\widehat{BAC}$ en utilisant le réultat précédent

    Solution

    $AB=\sqrt{x_{\overrightarrow{AB}}^2+y_{\overrightarrow{AB}}^2}=\sqrt{(-3)^2+(-4)^2}=\sqrt{25}=5$
    $AC=\sqrt{x_{\overrightarrow{AC}}^2+y_{\overrightarrow{AC}}^2}=\sqrt{(-5)^2+(-1)^2}=\sqrt{26}$
    $\overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos(\widehat{BAC})$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=5\times \sqrt{26}\times cos(\widehat{BAC})$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=5\sqrt{26}cos(\widehat{BAC})$
    On a donc l'égalité suivante:
    $\phantom{\Longleftrightarrow}5\sqrt{26}cos(\widehat{BAC})=19$
    $\Longleftrightarrow cos(\widehat{BAC})=\dfrac{19}{5\sqrt{26}}$
    donc $\widehat{BAC}=cos^{-1}\left( \dfrac{19}{5\sqrt{26}}\right)\approx 41,8^0 $
  4. On note $H$ le pied de la hauteur issue de $B$ dans $ABC$.
    Calculer $AH$.
    Donner la valeur exacte puis arrondie au mm près.

    Rappel de cours

    Produit scalaire et projeté orthogonal

    Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
    Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
    $\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
    et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)

    Aide

    $H$ est le projeté orthogonal de $A$ sur $(BC)$

    Solution

    $H$ le pied de la hauteur issue de $B$ dans $ABC$ donc $H\in (AC)$ et $(BH)\perp (AC)$
    donc $H$ est le projeté orthogonal de $B$ sur $(AC)$
    L'angle $\widehat{BAC}$ est aigu
    donc $\overrightarrow{AB}.\overrightarrow{AC}=AH\times AC=AH\sqrt{26}$
    On a donc:
    $\sqrt{26}AH=19$ donc $AH=\dfrac{19}{\sqrt{26}}$

vidéos semblables


Pour compléter ce devoir, nous vous conseillons les vidéos suivantes pour préparer ce devoir.
réf 902: Choisir la bonne expression du produit scalaire
| 3mnmn |

exercices semblables


Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
réf 874: Choisir la bonne expression
| 4-6mn |
réf 875: Calculs avec le produit scalaire
| 4-6mn |
réf 877: Calculs avec le produit scalaire et vecteurs orthogonaux
| 3-5mn |