---

Une entreprise organise une loterie pour ses employés pour les fêtes de fin d'année et on choisit au hasard un employé gagnant parmi l'ensemble des employés de l'entreprise.
La répartition des employés se fait de la façon suivante:
-$20$% des employés ont un diplôme en gestion des affaires
-$26$% des employés occupent un poste de cadre
-$70$% des diplômés en gestion des affaires ont des postes de cadre
On note:
- C désigne l'événement :"l'employé est un cadre"
- G désigne l'événement :"l'employé est diplôme en gestion des affaires"

1. Donner $p(C)$, $p(G)$ et $p_G(C)$

   Solution

   $20$% des employés ont un diplôme en gestion des affaires donc $p(G)=0,2$
   $26$% des employés occupent un poste de cadre donc $p(C)=0,26$
   $70$% des diplômés en gestion des affaires ont des postes de cadre donc $p_G(C)=0,7$
   $p(G)=0,2$, $p(C)=0,26$ et $p_G(C)=0,7$.
2. Compléter l'arbre pondéré correspondant aux divers cas possibles:
   

   Rappel de cours

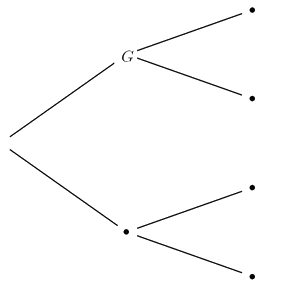
   Arbre pondéré

   ---

   Probabilités sur un arbre pondéré:
   

   Solution

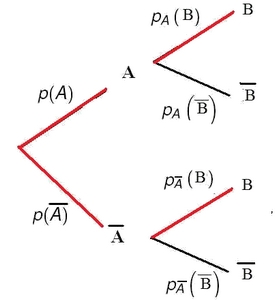   Arbre:
   
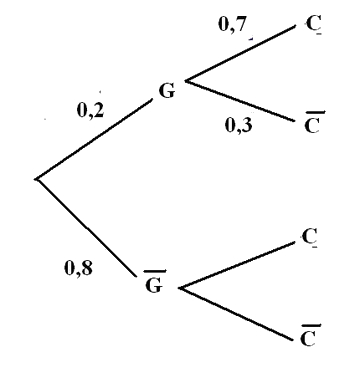
3. Calculer la probabilité de l'événement : "l'employé gagnant est un cadre et est diplômé en gestion des affaires".

   Rappel de cours

   Probabilité de l'événement $A\cap B$

   ---

   Soient $A$ et $B$ deux événements avec $p(A)\neq 0$, on a
   $p(A\cap B)=p(A)\times p_A(B)$

   Aide

   Cet événement se note $G\cap C$

   Solution

   L'événement :" l'employé gagnant est un cadre diplômé en gestion des affaires" se note $G\cap C$
   $p(C\cap G)=p(G)\times p_G(C)=0,2\times 0,7=0,14$
   La probabilité que l'employé gagnant soit un cadre et est diplômé en gestion des affaires est $p(C\cap G)=0,14$
4. Calculer la probabilité de l'événement: " l'employé gagnant est un cadre et n'est pas diplômé en gestion des affaires".

   Aide

   Cet événement se note $C\cap \overline{G}$
   Il faut utiliser la formule des probabilités totales pour $p(C)$

   Solution

   L'événement: "l'employé gagnant est un cadre sans diplôme en gestion des affaires" se note $C\cap \overline{G}$.
   D'après la formule des probabilités totales, on a:
   $\phantom{\Longleftrightarrow} p(C)=p(G\cap C)+p(\overline{G}\cap C )$
   
   $\Longleftrightarrow 0,26=0,14+p(\overline{G}\cap C )$
   
   $\Longleftrightarrow 0,12=p(\overline{G}\cap C )$
   La probabilité que l'employé gagnant soit un cadre et non diplômé en gestion des affaires est $p(\overline{G}\cap C )=0,12$
5. En déduire $p_{\overline{G}}(C)$

   Rappel de cours

   Probabilité conditionnelle

   ---

   Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
   La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
   et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.

   Solution

   $p_{\overline{G}}(C)=\dfrac{p(G\cap C)}{p(\overline{G})}=\dfrac{0,12}{?}$
   $p(\overline{G})=1-p(G)=1-0,2=0,8$
   donc $p_{\overline{G}}(C)=\frac{0,12}{0,8}=0,15$
   La probabilité que ce soit un cadre sachant qu'il n'a pas de diplôme en gestion des affaires se note $p_{\overline{G}}(C)=0,15$.
6. Le gagnant de la loterie est un cadre.
   Calculer la probabilité que ce soit un diplômé en gestion des affaires?

   Rappel de cours

   Probabilité conditionnelle

   ---

   Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
   La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
   et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.

   Aide

   On sait que l'employé est un cadre

   Solution

   La probabilité que le gagnant soit diplômé en gestion des affaires sachant que c'est un cadre se note $p_C(G)$.
   $p_C(G)=\dfrac{p(C\cap G)}{p(C)}=\frac{0,14}{0,26}\approx 0,54$
   La probabilité que le gagnant soit diplômé en gestion des affaires sachant que c'est un cadre est 0,54 environ.