Déterminer les limites suivantes:
- $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(x)}{x^3}$
Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes...Croissances comparées
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(x)}{x}=0$
$\displaystyle \lim_{x \rightarrow 0^+}xln(x)=0$On peut écrire $\dfrac{ln(x)}{x^3}=\dfrac{1}{x^2}\times \dfrac{ln(x)}{(x)}$Pour tout réel $x>0$ on a $\dfrac{ln(x)}{x^3}=\dfrac{1}{x^2}\times \dfrac{ln(x)}{(x)}$
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x^2}=0$
et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(x)}{x}=0$
donc par produit $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x^2}\times \dfrac{ln(x)}{x}=0$
Il s'agit bien d'un cas d'indétermination car $\displaystyle \lim_{x \rightarrow +\infty}ln(x)=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}x^3=+\infty$ - $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{x+1}{ln(x)}$
On a $\dfrac{x+1}{ln(x)}=\dfrac{x}{ln(x)}+\dfrac{1}{ln(x)}$Pour tout réel $x >0$ on a $\dfrac{x+1}{ln(x)}=\dfrac{x}{ln(x)}+\dfrac{1}{ln(x)}$
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(x)}{x}=0^+$ et donc la limite de l'inverse est $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{x}{ln(x)}=+\infty$
$\displaystyle \lim_{x \rightarrow +\infty}ln(x)=+\infty$ donc la limite de l'inverse est $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{ln(x)}=0$
Il s'agit bien d'un cas d'indétermination car $\displaystyle \lim_{x \rightarrow +\infty}x+1=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}ln(x)=+\infty$ - $\displaystyle \lim_{x \rightarrow 0^+}x^2ln(x)$
Croissances comparées
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(x)}{x}=0$
$\displaystyle \lim_{x \rightarrow 0^+}xln(x)=0$On a $(x^2+1)ln(x)=x^2ln(x)+ln(x)$Pour tout réel $x >0$ on a $x^2ln(x)=x\times xln(x)$
$\displaystyle \lim_{x \rightarrow 0^+}xln(x)=0$ et $\displaystyle \lim_{x \rightarrow 0^+}x=0$
donc par produit $\displaystyle \lim_{x \rightarrow 0^+}x\times xln(x)=\displaystyle \lim_{x \rightarrow 0^+}x^2ln(x)=0$
Il s'agit bien d'un cas d'indétermination car $\displaystyle \lim_{x \rightarrow 0^+}x^2=0$
et $\displaystyle \lim_{x \rightarrow 0^+}ln(x)=-\infty$ - $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(3x)}{x}$
Pour tout réel $x>0$ on a $\dfrac{ln(3x)}{x}=3\dfrac{ln(3x)}{3x}$Pour tout réel $x>0$ on a $\dfrac{ln(3x)}{x}=3\dfrac{ln(3x)}{3x}$
et $\displaystyle \lim_{x \rightarrow +\infty}3x=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(x)}{x}=0$
donc par composition on a $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(3x)}{3x}=0$
donc $\displaystyle \lim_{x \rightarrow +\infty}3\dfrac{ln(3x)}{3x}=0$
Pour éviter les confusions sur le variable $x$, on peut poser $X=3x$
Schématiquement, on a alors:
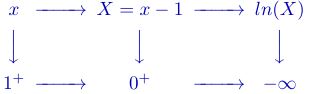
$\displaystyle \lim_{x \rightarrow +\infty}X=\displaystyle \lim_{x \rightarrow +\infty}3x=+\infty$
et $\displaystyle \lim_{X \rightarrow +\infty}\dfrac{ln(X)}{X}=0$
donc par composition on a $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(3x)}{3x}=0$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 1207
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Cours partie 2: dérivée et limites
- dérivée et limites de la fonction ln
- composition avec la fonction ln
infos cours
| 20mn
série 4 : Limites
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.