On considère les complexes $z=1+i$ et $z'=-1+i\sqrt{3}$.
- Déterminer l'écriture sous forme trigonométrique puis avec la notation exponentielle de $z$ et de $z'$
Forme trigonométrique
Soit $z=x+iY$ un complexe.
Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
Cette forme est appelée forme trigonométrique} de $z$.Forme exponentielle
$z$ est un complexe d'argument $\alpha$
La forme exponentielle de $z$ est $z=|z|e^{i\alpha}$$|z|=\sqrt{(1)^2+1^2}=\sqrt{2}$
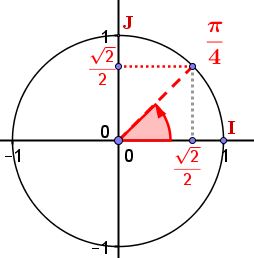
$z=\sqrt{2}\left(\dfrac{1}{\sqrt{2}}+i\dfrac{1}{\sqrt{2}}\right)$
$\phantom{z}=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+i\dfrac{\sqrt{2}}{2}\right)$
donc si on note $\theta=arg(z)$ on a:
$\begin{cases} cos(\theta)=\dfrac{\sqrt{2}}{2}\\ sin(\theta)=\dfrac{\sqrt{2}}{2} \end{cases}$
donc $\theta=\dfrac{\pi}{4}$ ($2\pi$) (c'est à dire $\theta=\dfrac{\pi}{4}+k2\pi$ avec $k \in \mathbb{Z}$).
$|z'|=\sqrt{(-1)^2+\sqrt{3}^2}=\sqrt{4}=2$
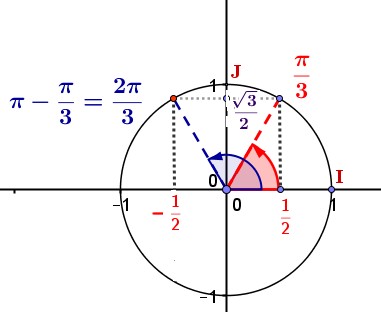
$z'=2\left(\dfrac{-1}{2}+i\dfrac{\sqrt{3}}{2}\right)$
donc si on note $\theta'=arg(z')$ on a:
$\begin{cases} cos(\theta')=\dfrac{-1}{2}\\ sin(\theta')=\dfrac{\sqrt{3}}{2} \end{cases}$
donc $\theta'=\dfrac{2\pi}{3}$ ($2\pi$) (c'est à dire $\theta'=\dfrac{2\pi}{3}+k2\pi$ avec $k \in \mathbb{Z}$).
- En utilisant la forme exponentielle, en déduire le module et l'argument de $zz'$.
$z=\sqrt{2}e^{i\frac{\pi}{4}}$ et $z'=2e^{i\frac{2\pi}{3}}$
$zz'=\sqrt{2}e^{i\frac{\pi}{4}}\times 2e^{i\frac{2\pi}{3}}$
$~~~~=2\sqrt{2}e^{i\frac{\pi}{4}+i\frac{2\pi}{3}}$
$~~~~=2\sqrt{2}e^{i\frac{3\pi}{12}+i\frac{8\pi}{12}}$
$~~~~=2\sqrt{2}e^{i\frac{11\pi}{12}}$
- Déterminer le module et l'argument de $\dfrac{z}{z'}$.
$\dfrac{z}{z'}=\dfrac{\sqrt{2}e^{i\frac{\pi}{4}}}{ 2e^{i\frac{2\pi}{3}}}$
$~~~~~=\dfrac{\sqrt{2}}{2}e^{i\frac{\pi}{4}-i\frac{2\pi}{3}}$
$~~~~~=\dfrac{\sqrt{2}}{2}e^{i\frac{3\pi}{12}-i\frac{8\pi}{12}}$
$~~~~~~=\dfrac{\sqrt{2}}{2}e^{-i\frac{5\pi}{12}}$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 1478
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Affixe - forme trigonométrique
- affixe d'un point et d'un vecteur
- complexes et géométrie
- forme trigoométrique
infos cours
| 20-25mn
série 4 : Forme trigonométrique, module et argument
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Déterminer la forme trigonométrique
- calcul du module
- calcul de l'argument
- exemples
infos: | 15-20mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.