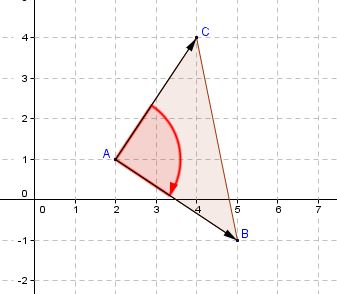
On donne les points $A$, $B$ et $C$ d'affixe respective $z_A=2+i$, $z_B=5-i$ et $z_C=4+4i$ dans un repère orthonormé $(O;\overrightarrow{i};\overrightarrow{j})$.
- Calculer l'affixe des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$.
Affixe d'un point et d'un vecteur
Le complexe $z=x+iy$ ($x$ et $y$ réels) est l'affixe du point $M(x;y)$. l Avec $\overrightarrow{u}(a;b)$, le complexe $u=a+ib$ est l'affixe du vecteur $\overrightarrow{u}$.$z_{\overrightarrow{AB}}=z_B-z_A=5-i-(2+i)=5-i-2-i=3-2i$
$z_{\overrightarrow{AC}}=z_C-z_A=4+4i-(2+i)=4+4i-2-i=2+3i$
- Ecrire le complexe $\dfrac{z_B-z_A}{z_C-z_A}$ sous forme algébrique.
Suppression des complexes au dénominateur
Pour écrire un nombre complexe sans complexes au dénominateur, il faut multiplier le numérateur et le dénominateur par le conjugué du dénominateur.
En effet $(a+ib)(a-ib)=a^2-iab+iba-i^2b^2=a^2+b^2$
soit $z\overline{z}=a^2+b^2$
Exemple:
$z=\dfrac{2+3i}{1-2i}=\dfrac{(2+3i)(1+2i)}{(1-2i)(1+2i)}=\dfrac{(2+3i)(1+2i)}{1+4}=\dfrac{(2+3i)(1+2i)}{5}$Il faut multiplier le numérateur et le dénominateur par le conjugué du complexe $z_C-z_A$.$\dfrac{z_B-z_A}{z_C-z_A}=\dfrac{3-2i}{2+3i}$
$\phantom{\dfrac{z_B-z_A}{z_C-z_A}}=\dfrac{(3-2i)(2-3i)}{(2+3i)(2-3i)}$
$\phantom{\dfrac{z_B-z_A}{z_C-z_A}}=\dfrac{6-9i-4i+6i^2}{2^2+3^2}$
$\phantom{\dfrac{z_B-z_A}{z_C-z_A}}=\dfrac{6-13i-6}{13}$
$\phantom{\dfrac{z_B-z_A}{z_C-z_A}}=\dfrac{-13i}{13}$
$\phantom{\dfrac{z_B-z_A}{z_C-z_A}}=-i$
- Calculer $AB$ et $AC$ et en déduire la nature du triangle $ABC$.
Distances et modules
Soient $A$ et $B$ d'affixes respectives $z_A$ et $z_B$.
$AB=|z_B-z_A|$Angles et argument d'un quotient
Soient $A$ , $B$ et $C$ quatre points distincts d'affixes respectives $z_A$, $z_B$ et $z_C$.
$(\overrightarrow{AB},\overrightarrow{AC})=arg\left(\dfrac{z_C-z_A}{z_B-z_A}\right)$Il faut calculer le module de $z_{\overrightarrow{AB}}$ et $z_{\overrightarrow{AC}}$ puis l'argument de $-i$$AB=|z_{\overrightarrow{AB}}|=\sqrt{3^2+(-2)^2}=\sqrt{13}$
$AC=|z_{\overrightarrow{AC}}|=\sqrt{2^2+3^2}=\sqrt{13}$
donc $ABC$ est isocèle en $A$.
$arg(-i)=\dfrac{-\pi}{2}$ ($2\pi$)
donc $(\overrightarrow{AC};\overrightarrow{AB})=arg\left(\dfrac{z_B-z_A}{z_C-z_A}\right)=-\dfrac{\pi}{2}$ ($2\pi$)
donc les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont orthogonaux
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 1478
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Affixe - forme trigonométrique
- affixe d'un point et d'un vecteur
- complexes et géométrie
- forme trigoométrique
infos cours
| 20-25mn
série 4 : Complexes et géométrie
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.