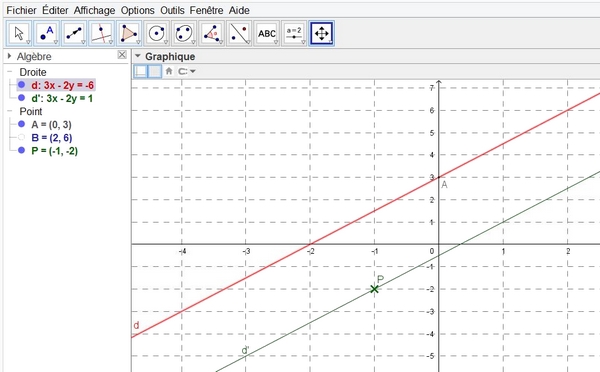
Dans le plan muni d'un repère orthogonal, on donne la droite $(d)$ d'équation $3x-2y+6=0$.
- Tracer $(d)$ dans un repère.
Vecteur directeur dans un repère
Dans un repère du plan, la droite $(d)$ a pour équation cartésienne $ax+by+c=0$ alors $\overrightarrow{u}(-b;a)$ est un vecteur directeur de $(d)$.
Si $(d)$ est définie par son équation réduite $y=ax+b$, $\overrightarrow{u}(1;a)$ est un vecteur directeur de $(d)$.
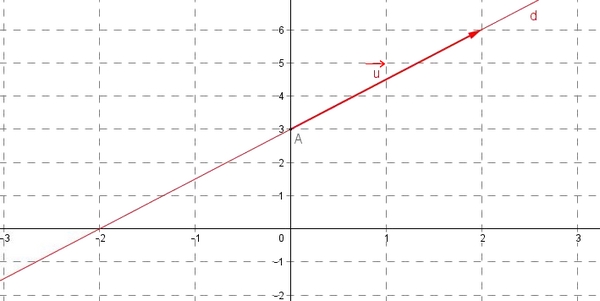
On peut utiliser un vecteur directeur de $(d)$ et les coordonnées d'un point $A$ de $(d)$ (à calculer)
Par exemple si $x_A=0$ calculer $y_A$On a ici $a=3$ et $b=-2$ donc $\overrightarrow{u}(2;3)$ est un vecteur directeur de $(d)$
Si $x=0$ alors on a $3\times 0-2y+6=0$
donc $y=\dfrac{-6}{-2}=3$
donc le point $A(0;3)$ appartient à $(d)$.
- Déterminer une équation cartésienne de la droite $(d')$ parallèle à $(d)$ et passant par $P(-1;-2)$
Droites parallèles
Deux droites parallèles ont des vecteurs directeurs colinéaires (ayant la même direction)Déterminer une équation cartésienne
Déterminer une équation cartésienne de la droite $(AB)$ avec $A(x_A;y_A)$ et $B(x_B;y_B)$ donnés dans un repère.
Méthode 1
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Si le point $M(x;y)$ appartient à $(AB)$, les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires
- $det(\overrightarrow{AM};\overrightarrow{AB})=0$
Méthode 2
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Les coordonnées de $\overrightarrow{AB}(-b;a)$ donnent les coefficients $a$ et $b$ d'une équation cartésienne
- $(AB)$: $ax+by+c=0$ et $A\in (AB)$ donc $ax_A+by_A+c=0$ (équation d'inconnue $c$)Un vecteur directeur de $(d)$ est aussi un vecteur directeur de $(d')$Rappel: $\overrightarrow{u}(2;3)$ est un vecteur directeur de $(d)$
Méthode 1
Soit $M(x;y)$ un point de $(d')$.
$\overrightarrow{PM}(x-(-1);y-(-2)$ soit $\overrightarrow{PM}(x+1;y+2$
$\overrightarrow{PM}$ et $\overrightarrow{u}$ colinéaires
$\Longleftrightarrow det(\overrightarrow{PM};\overrightarrow{u})=0$
$\Longleftrightarrow \begin{bmatrix} x+1&2\\ y+2&3\end{bmatrix}=0$
$\Longleftrightarrow 3(x+1)-2(y+2)=0$
$\Longleftrightarrow 3x+3-2y-4=0$
$\Longleftrightarrow 3x-2y-1=0$
Méthode 2:
$\overrightarrow{u}(2;3)$ est un vecteur directeur de $(d)$ donc de $(d')$.
$(d')$ admet une équation cartésienne de la forme $3x-2y+c'=0$
$P\in (d') \Longleftrightarrow 3x_P-2y_P+c'=0$
$~~~~~~~\Longleftrightarrow 3\times (-1)-2\times (-2)+c'=0$
$~~~~~~~\Longleftrightarrow -3+4+c'=0$
$~~~~~~~\Longleftrightarrow c'=-1$
- Contrôler les résultats en traçant les droites (avec GEOGEBRA par exemple)
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 438
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Équation cartésienne-vecteur directeur d'une droite
- vecteur directeur d'une droite
- équation cartésienne de droite
- déterminer une équation cartésienne
- équation cartésienne d'une parallèle
infos cours
| 20-30mn
série 6 : Droites parallèles
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Équations cartésiennes
- tracer une droite définie par son équation cartésienne
- déterminer une équation cartésienne
- déterminer si deux droites sont parallèles
- déterminer une équation cartésienne d'une parallèle
infos: | 20-25mn |
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.