- On veut définir une zone de baignade rectangulaire ouverte sur la plage et fermée sur trois côtés par une corde de longueur 100m. On veut déterminer les dimensions de cette zone pour que son aire soit maximale.
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$On peut poser $x$ et $y$ les longueurs des côtés de cette zone.
Il faut exprimer l'aire en fonction de $x$ en remplaçant $y$ par son expression en fonction de $x$On pose $x$ et $y$ les deux dimensions de ce rectangle.
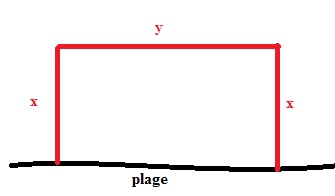
On a donc $2x+y=100$ soit $y=100-2x$.
L'aire de la zone de baignade est donc:
$\mathcal{A}(x)=x\times y=x(100-2x)=-2x^2+100x$
$\mathcal{A}(x)$ est une fonction polynôme de degré 2 avec $a=-2$, $b=100$ et $c=0$
$a<0$ donc le maximum (parabole à "l'envers") de $\mathcal{A}(x)$ est atteint pour $x=\dfrac{-b}{2a}=\dfrac{-100}{-4}=25$
On a alors $y=100-2x=100-50=50$ m.
On peut aussi dresser le tableau de variation de $\mathcal{A}(x)$ sachant que $x\in [0;50]$ car on doit avoir $2x\leq 100$ - $AMEF$ et $MBCD$ sont des carrés avec $AB=10$ cm et $M\in [AB]$.
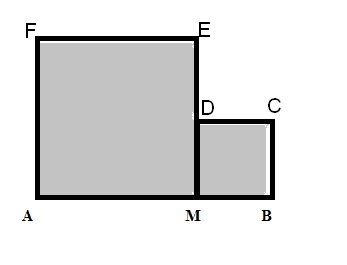
Déterminer la position de $M$ pour que l'aire totale(en gris ) soit maximale.Il faut exprimer l'aire totale (somme des aires des deux carrés) en fonction de $x=AM$ avec $0\leq x \leq 10$On pose $AM=x$ donc $MB=10-x$ et on doit avoir $x\in [0;10]$.
L'aire de $AMEF$ est $A_1=x^2$ et celle de $MBDC$ est $A_2=(10-x)^2$.
L'aire totale de la zone grise est donc: $A(x)=A_1+A_2=x^2+(10-x)^2$
$\phantom{A(x)=A_1+A_2}=x^2+100-20x+x^2$
$\phantom{A(x)=A_1+A_2}=2x^2-20x+100$
$A(x)$ est donc une fonction polynôme du second degré avec $a=2$, $b=-20$ et $c=100$.
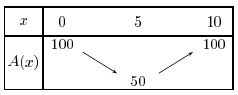
L'abscisse du sommet de la parabole représentant $A(x)$ est $\alpha=\dfrac{-b}{2a}=\dfrac{20}{4}=5$ et son ordonnée est $\beta=A(5)=2\times 5^2-20\times 5+100=50-100+100=50$
On a $a>0$ donc le tableau de variation de $A$ est le suivant:
- Existe-t-il deux entiers dont le produit est 218 et la somme 30?
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Il faut écrire deux égalités avec $x$ et $y$ les deux nombres cherchés et se ramener à une équation à une inconnue par substitution.On pose $x$ et $y$ les deux entiers cherchés.
$\begin{cases} x+y=30\\ xy=218 \end{cases} \Longleftrightarrow \begin{cases} y=30-x\\ x(30-x)=218 ~~~\text{on se ramène à une équation à une inconnue} \end{cases}$
$\phantom{\begin{cases} x+y=30\\ xy=218 \end{cases}} \Longleftrightarrow \begin{cases} y=30-x\\ -x^2+30x-218=0 \end{cases}$
Résolution de $-x^2+30x-218=0$
$\Delta=b^2-4ac=30^2-4\times (-1)\times (-218)=28$
$\Delta>0$ donc il y a deux racines
$x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{ -30+\sqrt{28} }{-2 }=\dfrac{-30+2\sqrt{7}}{-2}=15-\sqrt{7}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{ -30- \sqrt{28}}{-2 }=15+\sqrt{7}$
Il y a deux solutions à cette équations mais $x$ est un entier
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 660
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Discriminant et racines
- discriminant
- racines d'un polynôme du second degré
- somme et produit des racines
- cas où le calcul du discriminant est inutile
infos cours
| 15-20mn
série 6 : Synthèse et problèmes de recherhe
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.