$ABCD$ est un trapèze (voir figure ci-dessous) tel que $AB=7$ cm, $AD=5$cm et $CD=2$cm
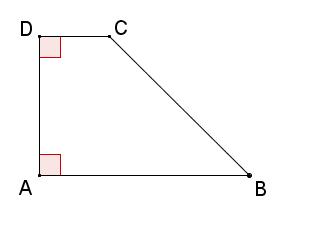
- Calculer $ \overrightarrow{AB}. \overrightarrow{CD}$.
Produit scalaire (définition)
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
$\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$On peut construire $B'$ tel que $\overrightarrow{CB'}=\overrightarrow{CB}$On construit $B'$ tel que $\overrightarrow{CB'}=\overrightarrow{CB}$
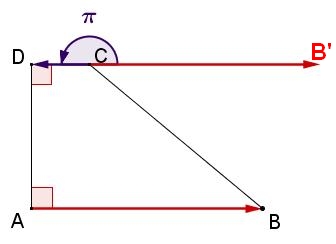
donc $\widehat{BCB'}=\pi$
et $cos(\pi)=-1$
$ \overrightarrow{AB}. \overrightarrow{CD}= \overrightarrow{CB'}. \overrightarrow{CD}$ $\phantom{ \overrightarrow{AB}. \overrightarrow{CD}}=|| \overrightarrow{CB'}||\times || \overrightarrow{CD}||\times cos( \widehat{CDB'})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{CD}}=AB \times CD\times cos(\pi)$
$\phantom{ \overrightarrow{AB}. \overrightarrow{CD}}=7\times 2\times (-1)$
$\phantom{ \overrightarrow{AB}. \overrightarrow{CD}}=-14$
- Calculer $ \overrightarrow{BA}. \overrightarrow{BC}$.
Produit scalaire et projeté orthogonal
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)Soit $H$ le projeté orthogonal de $C$ sur $(AB)$, déterminer la nature du triangle $BHC$
Utiliser le point $H$ et les distances $BA$ et $BH$Soit $H$ le projeté orthogonal de $C$ sur $(AB)$, on a alors $CH=DA=5$cm
et $BH=BA-HA=BA-CD=5$cm
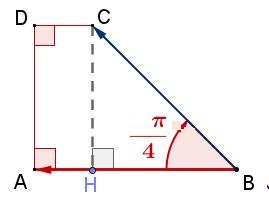
$ \overrightarrow{BA}. \overrightarrow{BC}=|| \overrightarrow{BA}||\times || \overrightarrow{BC}||\times cos( \widehat{ABC})$
$\phantom{ \overrightarrow{BA}. \overrightarrow{BC}}=BA\times BH$
$\phantom{ \overrightarrow{AB}. \overrightarrow{BC}}=7\times 5$
$\phantom{ \overrightarrow{BA}. \overrightarrow{BC}}=35$
- Calculer $ \overrightarrow{AD}. \overrightarrow{CB}$.
Soit $B'$ tel que $ \overrightarrow{AB'}= \overrightarrow{CB}$ (voir figure)
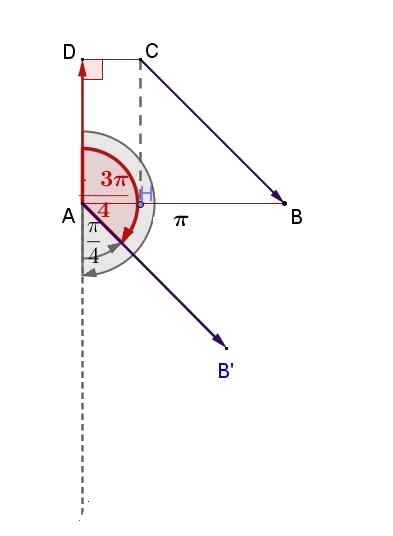
donc $\widehat{B'AD}=\dfrac{3\pi}{4}$
$\dfrac{3\pi}{4}=\pi-\dfrac{\pi}{4}$
Sur le cercle trigonométrique, les points correspondant aux mesures $\dfrac{\pi}{4}$ et $\dfrac{3\pi}{4}$ sont symétriques par rapport à l'axe des ordonnées
donc $cos(\dfrac{3\pi}{4})=-cos(\dfrac{\pi}{4})=-\dfrac{\sqrt{2}}{2}$
Dans $BHC$ rectangle en $H$ on a:
$BC^2=AH^2+HB^2=5^2+5^2=50$
donc $BC=\sqrt{50}=5\sqrt{2}$
$ \overrightarrow{AD}. \overrightarrow{CB}=|| \overrightarrow{AD}||\times || \overrightarrow{CB}||\times cos( \overrightarrow{AD}, \overrightarrow{CB})$
$\phantom{ \overrightarrow{AD}. \overrightarrow{CB}}=AD\times CB \times cos(\dfrac{3\pi}{4})$
$\phantom{ \overrightarrow{AD}. \overrightarrow{CB}}=5\times 5\sqrt{2}\times \dfrac{-\sqrt{2}}{2}$
$\phantom{ \overrightarrow{AD}. \overrightarrow{CB}}=-\dfrac{50}{2}=-25$

donc $\widehat{B'AD}=\dfrac{3\pi}{4}$
$\dfrac{3\pi}{4}=\pi-\dfrac{\pi}{4}$
Sur le cercle trigonométrique, les points correspondant aux mesures $\dfrac{\pi}{4}$ et $\dfrac{3\pi}{4}$ sont symétriques par rapport à l'axe des ordonnées
donc $cos(\dfrac{3\pi}{4})=-cos(\dfrac{\pi}{4})=-\dfrac{\sqrt{2}}{2}$
Dans $BHC$ rectangle en $H$ on a:
$BC^2=AH^2+HB^2=5^2+5^2=50$
donc $BC=\sqrt{50}=5\sqrt{2}$
$ \overrightarrow{AD}. \overrightarrow{CB}=|| \overrightarrow{AD}||\times || \overrightarrow{CB}||\times cos( \overrightarrow{AD}, \overrightarrow{CB})$
$\phantom{ \overrightarrow{AD}. \overrightarrow{CB}}=AD\times CB \times cos(\dfrac{3\pi}{4})$
$\phantom{ \overrightarrow{AD}. \overrightarrow{CB}}=5\times 5\sqrt{2}\times \dfrac{-\sqrt{2}}{2}$
$\phantom{ \overrightarrow{AD}. \overrightarrow{CB}}=-\dfrac{50}{2}=-25$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 866
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Expressions du produit scalaire (part1)
- définition du produit scalaire
- produit scalaire et projeté orthogonal
- utilisation des normes
- produit scalaire dans un repère orthonormé
infos cours
| 20-25mn
série 2 : Utilisation des différentes expressions
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.