1. Home
  2. chapitre 6 Produit scalaire
  3. exercice corrigé nº883
PDF reservé aux abonnés vidéo de l'exercice
  1. $ABC$ est un triangle tel que $AB=6$cm et $AC=5$cm et $\widehat{BAC}=\dfrac{\pi}{6}$
    Calculer $BC$

    Rappel de cours

    Produit scalaire (définition)

    $\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
    $\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$

    Produit scalaire avec les normes

    Pour tous vecteurs $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$ on a:
    $\overrightarrow{u}.\overrightarrow{v}=\dfrac{\mid \mid \overrightarrow{u}\mid \mid^2+\mid \mid \overrightarrow{v}\mid \mid^2-\mid \mid \overrightarrow{u}-\overrightarrow{v}\mid \mid^2}{2}$
    Dans le triangle $ABC$: $\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$

    Aide

    Calculer $ \overrightarrow{AB}. \overrightarrow{AC}$ en utilisant les distances $AB$, $AC$ et l'angle $\widehat{BAC}$
    Utiliser le rappel de cours ci dessus en calculant $ \overrightarrow{AB}. \overrightarrow{AC}$ puis écrire une équation d'inconnue $BC^2$ en utilisant les deux résultats obtenus pour $ \overrightarrow{AB}. \overrightarrow{AC}$

    Solution

    $\overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos( \overrightarrow{AB}, \overrightarrow{AC})$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=6\times 5 \times cos(\dfrac{\pi}{6})$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=30 \times \dfrac{\sqrt{3}}{2}$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=15\sqrt{3}$


    $\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=\dfrac{6^2+5^2-BC^2}{2}$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=\dfrac{61-BC^2}{2}$

    Il faut donc résoudre l'équation $\dfrac{61-BC^2}{2}=15\sqrt{3}$
    $\phantom{\Longleftrightarrow}\dfrac{61-BC^2}{2}=15\sqrt{3}$
    $\Longleftrightarrow 61-BC^2=2\times 15\sqrt{3}$
    $\Longleftrightarrow -BC^2=30\sqrt{3}-61$
    $\Longleftrightarrow BC^2=-30\sqrt{3}+61$
    $BC$ est une longueur donc $BC=\sqrt{61-30\sqrt{3}}$
  2. $ABC$ est un triangle tel que $AB=6$cm et $AC=2\sqrt{13}$cm et $\widehat{ABC}=\dfrac{\pi}{3}$
    Calculer $BC$

    Rappel de cours

    Racines

    Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
    c'est à dire telles que $P(x)=0$.
    $\Delta=b^2-4ac$
    Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
    Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
    Si $\Delta<0$ il n'y a aucune racine
    Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.

    Aide

    L'angle donné est l'angle de sommet $B$ donc il faut utiliser le produit scalaire des vecteurs $ \overrightarrow{BA}$ et $ \overrightarrow{BC}$
    Calculer $ \overrightarrow{AB}. \overrightarrow{AC}$ en utilisant les distances $AB$, $AC$ et l'angle $\widehat{ABC}$
    Exprimer ensuite $ \overrightarrow{BA}. \overrightarrow{BC}$ en fonction des distances $AB$, $AC$ et $BC$ puis écrire une équation d'inconnue $BC^2$ en utilisant les deux résultats obtenus pour $ \overrightarrow{BA}. \overrightarrow{BC}$

    Solution

    figure

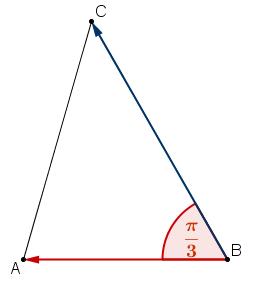
    $\overrightarrow{BA}.\overrightarrow{BC}=BA\times BC\times cos( \overrightarrow{BA}, \overrightarrow{BC})$
    $\phantom{\overrightarrow{BA}.\overrightarrow{BC}}=6\times BC \times cos(\dfrac{\pi}{3})$
    $\phantom{\overrightarrow{BA}.\overrightarrow{BC}}=6 \times BC\times \dfrac{1}{2}$
    $\phantom{\overrightarrow{BA}.\overrightarrow{BC}}=3BC$


    $ \overrightarrow{BA}- \overrightarrow{BC}= \overrightarrow{BA}+ \overrightarrow{CB}= \overrightarrow{CA}$
    $\overrightarrow{BA}.\overrightarrow{BC}=\dfrac{BA^2+BC^2-CA^2}{2}$
    $\phantom{\overrightarrow{BA}.\overrightarrow{BC}}=\dfrac{6^2+BC^2-4\times 13}{2}$
    $\phantom{\overrightarrow{AB}.\overrightarrow{AC}}=\dfrac{-16+BC^2}{2}$

    Il faut donc résoudre l'équation $\dfrac{-16+BC^2}{2}=3BC$
    $\phantom{\Longleftrightarrow} -16+BC^2=6BC$
    $\Longleftrightarrow BC^2-6BC-16=0$
    Recherche des racines du polynôme $x^2-6x-16$:
    $\Delta=b^2-4ac=(-6)^2-4\times 1\times (-16)=100$
    $\Delta>0$ donc il y a deux racines: $x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{6-10}{2}=-2$ et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{6+10}{2}=8$
    $BC$ est une longueur donc $BC\geq 0$
    donc $ BC=x_2=8$cm
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
valider cet exercice
marquer cet exercice à revoir

Cours nº 868


Vous pouvez retourner sur le cours après avoir vu cette vidéo.

Applications

- théorème de la médiane
- caractérisation du cercle
- calculs d'angles dans un triangle

infos cours

| 15mn
série 3 : Calculs d'angles et d longueurs

retour sur le cours

Fiche méthode


Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.

Calculs de longueurs et d'angles dans un triangle

- calcul d'une longueur
- calcul d'un angle

infos: | 10-15mn |

PDF reservé aux abonnés

exercices semblables


Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.
Longueur de la diagonale d'un rectangle
| 10-15mn |