On donne les points $A$ et $B$ tels que $AB=6$cm.
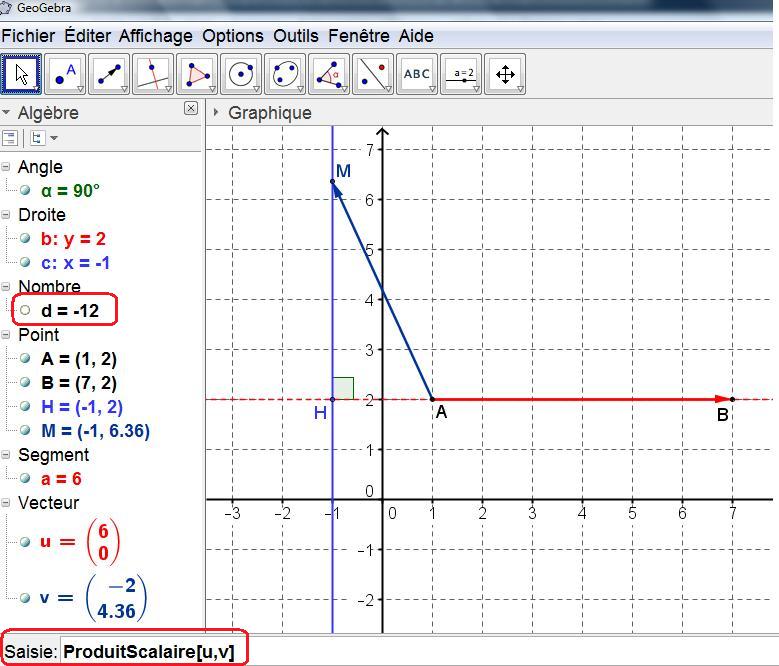
- Déterminer et représenter l'ensemble des points $M$ du plan tels que $ \overrightarrow{AM}. \overrightarrow{AB}=-12$
Produit scalaire et projeté orthogonal
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)Utiliser le projeté orthogonal de $M$ sur $(AB)$Soit $H$ le projeté orthogonal de $M$ sur $(AB)$
$ \overrightarrow{AM}. \overrightarrow{AB}<0$ donc $H\notin [AB)$ et l'angle $\widehat{BAM}$ est obtus.
On a alors $ \overrightarrow{AM}. \overrightarrow{AB}=-AH\times AB=-6AH$ car $AB=6$
$ \overrightarrow{AM}. \overrightarrow{AB}=-12 \Longleftrightarrow -6AH=-12 \Longleftrightarrow AH=2$
donc les points $M$ dont le projeté orthogonal est $H$ sur $(AB)$ avec $AH=2$ et $H\notin [AB)$ vérifient $ \overrightarrow{AM}. \overrightarrow{AB}=-12$
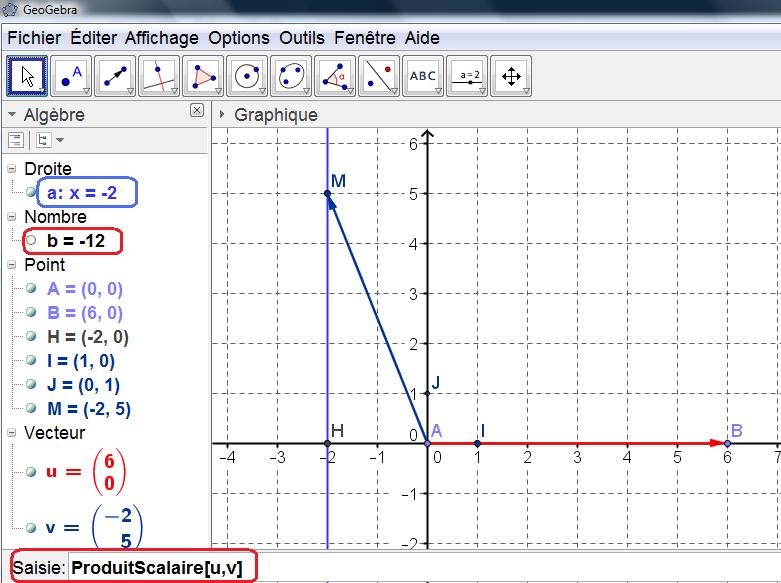
Avec le point $I$ défini par $ \overrightarrow{AI}=\dfrac{1}{6} \overrightarrow{AB}$ et le point $J$ tel que $ \overrightarrow{AJ}$ et $ \overrightarrow{AI}$ sont orthogonaux et $AI=AJ$
Le repère $(A; \overrightarrow{AI}; \overrightarrow{AJ})$ est orthonormé.
En notant $x$ et $y$ les coordonnées de $M$ dans ce repère, on a:
$ \overrightarrow{AB}(6;0)$, $AB=6$ unités (l'unité étant alors le centimètre) et $ \overrightarrow{AM}(x;y)$
$ \overrightarrow{AM}. \overrightarrow{AB}=-12 \Longleftrightarrow x_{ \overrightarrow{AM}}x_{ \overrightarrow{AB}}+y_{ \overrightarrow{AM}}y_{ \overrightarrow{AB}}=-12$
$\phantom{ \overrightarrow{AM}. \overrightarrow{AB}=-12} \Longleftrightarrow x\times 6+y\times 0=-12$
$\phantom{ \overrightarrow{AM}. \overrightarrow{AB}=-12} x=-2$
$x=-2$ est une équation de la droite parallèle à l'axe des ordonnées passant par le point $H(-2;0)$
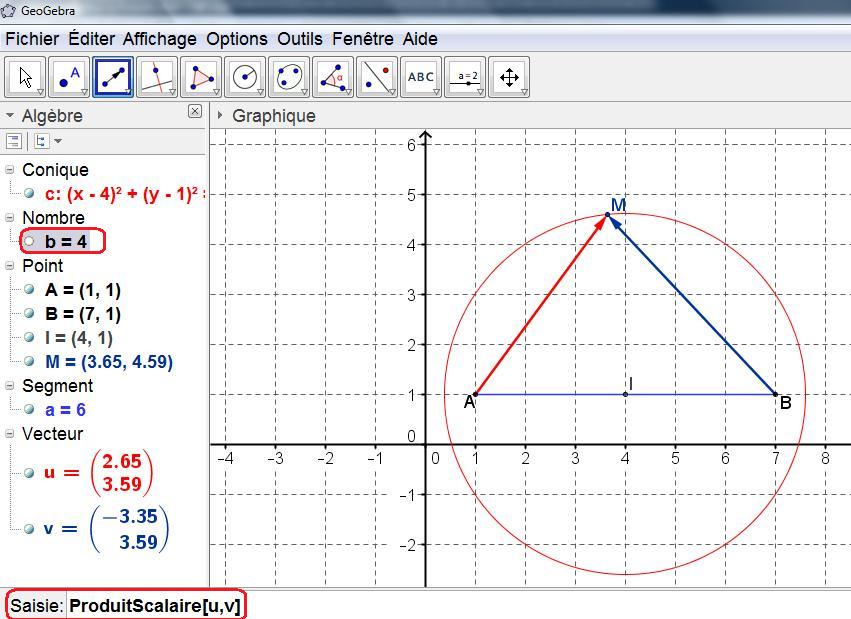
- Déterminer et représenter l'ensemble des points $M$ du plan tels que $ \overrightarrow{AM}. \overrightarrow{BM}=4$
Carré scalaire
$\overrightarrow{u}^2=\overrightarrow{u}.\overrightarrow{u}=||\overrightarrow{u}||^2$Utiliser le point $I$ milieu de $[AB]$
Décomposer $ \overrightarrow{AM}= \overrightarrow{AI}+ \overrightarrow{IM}$ et $ \overrightarrow{BM}= \overrightarrow{BI}+ \overrightarrow{IM}$ puis développer l'expressionSoit $I$ le milieu de $[AB]$, on a alors $ \overrightarrow{AI}= \overrightarrow{IB}=\dfrac{1}{2} \overrightarrow{AB}$ et $ \overrightarrow{AI}+ \overrightarrow{BI}= \overrightarrow{0}$
$ \overrightarrow{AM}. \overrightarrow{BM}=4 \Longleftrightarrow ( \overrightarrow{AI}+ \overrightarrow{IM}).( \overrightarrow{BI}+ \overrightarrow{IM})=4$
$\phantom{ \overrightarrow{AM}. \overrightarrow{BM}=4} \Longleftrightarrow \overrightarrow{AI}. \overrightarrow{BI}+ \overrightarrow{IM}. \overrightarrow{BI}+ \overrightarrow{AI}. \overrightarrow{IM}+ \overrightarrow{IM}. \overrightarrow{IM}=4$
$\phantom{ \overrightarrow{AM}. \overrightarrow{BM}=4} \Longleftrightarrow (\dfrac{1}{2} \overrightarrow{AB}).(-\dfrac{1}{2} \overrightarrow{AB})+ \overrightarrow{IM}. \overrightarrow{BI}+ \overrightarrow{IM}. \overrightarrow{AI}+ \overrightarrow{IM}^2=4$
$\phantom{ \overrightarrow{AM}. \overrightarrow{BM}=4} \Longleftrightarrow \dfrac{-1}{4} \overrightarrow{AB}^2+ \overrightarrow{IM}.( \overrightarrow{BI}+ \overrightarrow{AI})+ \overrightarrow{IM}^2=4$
$\phantom{ \overrightarrow{AM}. \overrightarrow{BM}=4} \Longleftrightarrow \dfrac{-1}{4}AB^2+ \overrightarrow{IM}. \overrightarrow{0}+IM^2=4$
$\phantom{ \overrightarrow{AM}. \overrightarrow{BM}=4} \Longleftrightarrow \dfrac{-36}{4}+IM^2=4$
$\phantom{ \overrightarrow{AM}. \overrightarrow{BM}=4} \Longleftrightarrow IM^2=4 +9$
$\phantom{ \overrightarrow{AM}. \overrightarrow{BM}=4} \Longleftrightarrow IM^2=13$
$\phantom{ \overrightarrow{AM}. \overrightarrow{BM}=4} \Longleftrightarrow IM=\sqrt{13}$ car $IM\geq 0$ ($IM$ est une distance)
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 868
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Applications
- théorème de la médiane
- caractérisation du cercle
- calculs d'angles dans un triangle
infos cours
| 15mn
série 3 : Execrices de synthèse
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.