Le plan est muni d'un repère orthonormé et on donne les points $A(1;4)$ et $B(-3;6)$.
- Déterminer et représenter l'ensemble des points $M(x;y)$ du plan tels que $ \overrightarrow{AM}. \overrightarrow{AB}=1$
Coordonnées d'un vecteur défini par deux points
Si $A(x_A;y_A)$ et $B(x_B;y_B)$ alors $\overrightarrow{AB}(x_B-x_A;y_B-y_A)$ (coordonnées du second point $-$ coordonnées du premier point)Produit scalaire dans un repère orthonormé
Dans un repère orthonormé, si $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ on a:
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'$
Calculer les coordonnées des vecteurs $ \overrightarrow{AM}$ et $ \overrightarrow{AB}$
Calculer $ \overrightarrow{AM}. \overrightarrow {AB}$ pour obtenir une relation de la forme $ax+by+c=0$ (équation cartésienne d'une droite)$\begin{cases} x_{ \overrightarrow{AM}}=x_M-x_A=x-1 \\ y_{ \overrightarrow{AM}}=y_M-y_A= y-4 \end{cases}$
donc $ \overrightarrow{AM}( x-1 ; y-4 )$
$\begin{cases} x_{ \overrightarrow{AB}}=x_B-x_A=-3-1 =-4 \\ y_{ \overrightarrow{AB}}=y_B-y_A= 6-4 = 2 \end{cases}$
donc $ \overrightarrow{AB}( -4 ; 2 )$
$\phantom{\Longleftrightarrow} \overrightarrow{AM}. \overrightarrow{AB}=1$
$\Longleftrightarrow x_{ \overrightarrow{AM}}x_{ \overrightarrow{AB}}+y_{ \overrightarrow{AM}}y_{ \overrightarrow{AB}}=1$
$\Longleftrightarrow (x-1)\times (-4)+(y-4)\times 2=1$
$\Longleftrightarrow -4x+4+2y-8=1$
$\Longleftrightarrow -4x+2y-5=0$
L'ensemble des points $M$ tels que $ \overrightarrow{AM}. \overrightarrow{AB}=1$ est la droite d'équation $-4x+2y-5=0$
L'équation réduite de cette droite est $y=\dfrac{4x+5}{2}=2x+\dfrac{5}{2}$
Avec GEOGEBRA, on peut placer les points $A$ et $B$, tracer la droite d'équation $-4x+2y-5=0$ puis tracer les vecteurs $ \overrightarrow{u}= \overrightarrow{AB}$ et $ \overrightarrow{v}= \overrightarrow{AM}$ avec $M\in(d)$
puis utiliser la commande ProduitScalaire[u,v](voir image ci-dessous)
pour vérifier que $ \overrightarrow{AM}. \overrightarrow{AB}=1$
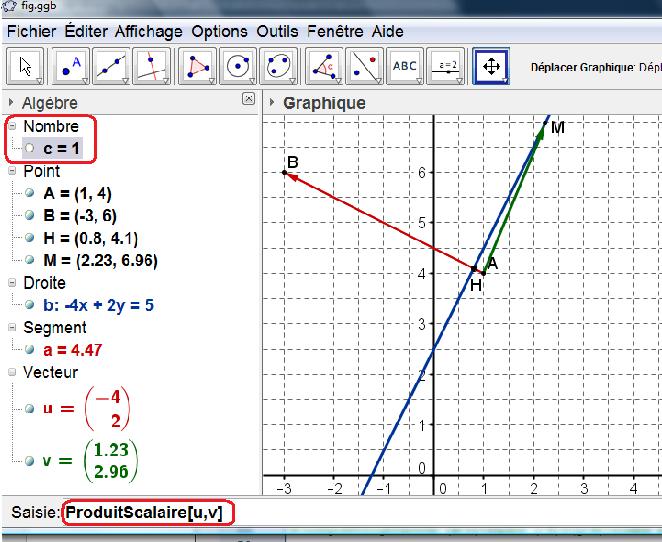
Pour tracer la droite dans un repère, on peut chercher les coordonnées de deux points $D_1$ et $D_2$ de cette droite:
Par exemple, si $x=0$, on a $2y-5=0 \Longleftrightarrow y=\dfrac{5}{2}$ donc $D_1(0;2,5)$
et si $x=-2$, on a $8+2y-5=0 \Longleftrightarrow y=\dfrac{-3}{2}$ donc $D_2(-2;-1,5)$ - Montrer que les coordonnées de $M(x;y)$ du plan tels que $ \overrightarrow{AM}. \overrightarrow{BM}=1$ doivent vérifier l'égalité $x^2+2x+y^2-10y+20=0$.
Montrer que $x^2+2x+y^2-10y+20=0\Longleftrightarrow (x+1)^2+(y-5)^2=6$ et en déduire l'ensemble des points $M$ vérifiant $\overrightarrow{AM}. \overrightarrow{BM}=1$.Distance dans un repère
Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$Exprimer les coordonnées des vecteurs $ \overrightarrow{AM}$ et $ \overrightarrow{BM}$ en fonction de $x$ et $y$
On a alors $MC^2$ avec $C(-1;5)$$\begin{cases} x_{ \overrightarrow{AM}}=x_M-x_A=x-1 \\ y_{ \overrightarrow{AM}}=y_M-y_A= y-4 \end{cases}$
donc $ \overrightarrow{AM}( x-1 ; y-4 )$
$\begin{cases} x_{ \overrightarrow{BM}}=x_M-x_B=x-(-3)=x+3 \\ y_{ \overrightarrow{BM}}=y_M-y_B= y-6 \end{cases}$
donc $ \overrightarrow{BM}( x+3 ; y-6 )$
$\phantom{\Longleftrightarrow} \overrightarrow{AM}. \overrightarrow{BM}=1$
$\Longleftrightarrow x_{ \overrightarrow{AM}}x_{ \overrightarrow{BM}}+y_{ \overrightarrow{AM}}y_{ \overrightarrow{BM}}=1$
$\Longleftrightarrow (x-1)(x+3)+(y-4)(y-6)=1$
$\Longleftrightarrow x^2+3x-x-3+y^2-4y-6y+24=1$
$\Longleftrightarrow x^2+2x+y^2-10y+20=0$
$(x+1)^2+(y-5)^2=6 \Longleftrightarrow x^2+2x+1+y^2-10y+25=6$
$\phantom{(x+1)^2+(y-5)^2=6} \Longleftrightarrow x^2+2x+y^2-10y+26-6=0$
$\phantom{(x+1)^2+(y-5)^2=6} \Longleftrightarrow x^2+2x+y^2-10y+20=0$
Si on pose $C(-1;5)$ alors $CM^2=(x_M-x_C)^2+(y_M-y_C)^2=(x+1)^2+(y-5)^2$
et on veut donc $CM^2=6$ soit $CM=\sqrt{6}$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 868
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Applications
- théorème de la médiane
- caractérisation du cercle
- calculs d'angles dans un triangle
infos cours
| 15mn
série 3 : Execrices de synthèse
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.