$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=-1-1=-2 \\ y_{\overrightarrow{AB}}=y_B-y_A=3-2=1 \\ \end{cases}$
$\overrightarrow{AB}(-2;1)$ est un vecteur directeur de $(AB)$
$\overrightarrow{AB}(-b;a)$ est un vecteur directeur de $(AB)$
donc $a=1$ et $b=2$.
Une équation cartésienne de $(AB)$ est de la forme $x+2y+c=0$
$A\in (AB)\Longleftrightarrow x_A+2y_A+c=0$
$~~~~~~~\Longleftrightarrow 1+4+c=0$
$~~~~~~~\Longleftrightarrow c=-5$
$-x-2y+5=0$ est une équation cartésienne de la droite (AB)
Remarques
Il existe une infinité d'équations cartésiennes pour une même droite.
Par exemple $-x-2y+5=0\Longleftrightarrow x+2y-5=0\Longleftrightarrow 2x+4y-10=0$ sont deux autres équations cartésiennes possibles de (d).
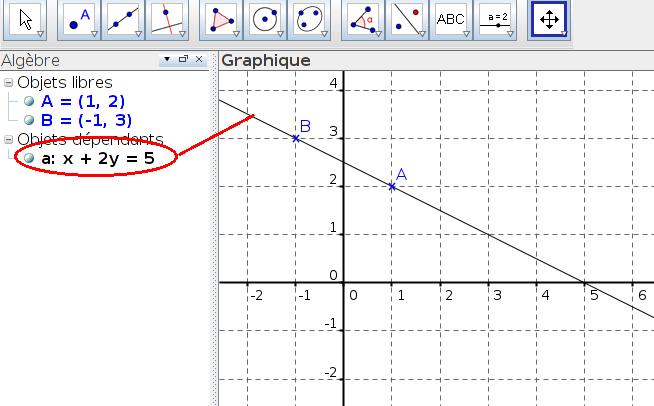
On peut utiliser également GEOGEBRA pour contrôler le résultat car une équation de la droite tracée est affichée dans la fenêtre algèbre
On peut aussi vérifier avec la calculatrice que les coordonnées des deux point de l'énoncé vérifie l'équation de droite obtenue.

Autre méthode: avec le critère de colinéarité:
Soit $M(x;y)$ un point de la droite $(AB)$.
$\begin{cases} x_{\overrightarrow{AM}}=x_M-x_A=x-1 \\ y_{\overrightarrow{AM}}=y_M-y_A=y-2 \\ \end{cases}$
$\overrightarrow{AM}(x-1;y-2)$
$M\in (AB)$
$\Longleftrightarrow \overrightarrow{AB}$ et $\overrightarrow{AM}$ colinéaires
$\Longleftrightarrow x_{\overrightarrow{AB}}y_{\overrightarrow{AM}}- y_{\overrightarrow{AB}}x_{\overrightarrow{AM}}=0$
$\Longleftrightarrow -2(y-2)-1(x-1)=0$
$\Longleftrightarrow -2y+4-x+1=0$
$\Longleftrightarrow -x-2y+5=0$

$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=-2-(-1)=-1 \\ y_{\overrightarrow{AB}}=y_B-y_A=3-(-1)=4\\ \end{cases}$
$\overrightarrow{AB}(-1;4)$ est un vecteur directeur de $(AB)$
$\overrightarrow{AB}(-b;a)$ est un vecteur directeur de $(AB)$
donc $a=4$ et $b=1$.
Une équation cartésienne de $(AB)$ est de la forme $4x+y+c=0$
$A\in (AB)\Longleftrightarrow 4x_A+y_A+c=0$
$~~~~~~~\Longleftrightarrow -4+3+c=0$
$~~~~~~~\Longleftrightarrow c=1$
$4x+y+1=0$ est une équation cartésienne de $(AB)$