Dans le plan muni d'un repère orthogonal, déterminer dans chaque cas une équation cartésienne de la droite $(d)$ passant par $A$ et de vecteur directeur $\overrightarrow{u}$
- $A(1;2)$ et $\overrightarrow{u}(-1;3)$
Déterminer une équation cartésienne
Déterminer une équation cartésienne de la droite $(AB)$ avec $A(x_A;y_A)$ et $B(x_B;y_B)$ donnés dans un repère.
Méthode 1
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Si le point $M(x;y)$ appartient à $(AB)$, les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires
- $det(\overrightarrow{AM};\overrightarrow{AB})=0$
Méthode 2
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Les coordonnées de $\overrightarrow{AB}(-b;a)$ donnent les coefficients $a$ et $b$ d'une équation cartésienne
- $(AB)$: $ax+by+c=0$ et $A\in (AB)$ donc $ax_A+by_A+c=0$ (équation d'inconnue $c$)$\overrightarrow{u}(-b;a)$ est un vecteur directeur de la droite (d)
Déteriminer $A$ et $b$ puis $c$ avec les coordonnées de $A$$\overrightarrow{u}(-1;3)$ est un vecteur directeur de $(d)$
et si $ax+by+c=0$ est une équation cartésienne de (d), le vecteur $\overrightarrow{u}(-b;a)$ est un vecteur directeur de (d)
donc ici $-b=-1$ soit $b=1$ et $a=3$ donc une équation cartésienne de $(d)$ est de la forme $3x+y+c=0$
On peut utiliser les les coordonnées du point $A$ pour calculer $c$:
$A\in (AB)\Longleftrightarrow 3x_A+y_A+c=0\Longleftrightarrow 3+2+c=0\Longleftrightarrow c=-5$
On peut utiliser GEOGEBRA pour afficher une équation dans la fenêtre algèbre. Il suffit de placer le point A, le vecteur $\overrightarrow{u}$ puis tracer la droite et lire une équation de celle-ci affichée dans la fenêtre algèbre.
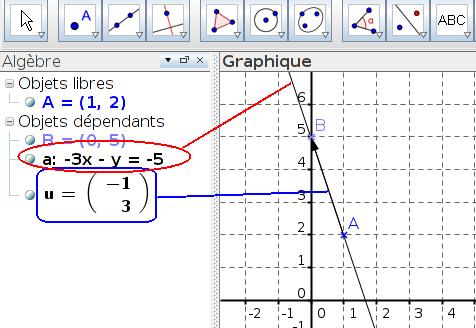
Il existe une infinité d'équations cartésiennes pour une même droite.
Par exemple $-3x-y+5=0\Longleftrightarrow 3x+y-5=0\Longleftrightarrow 6x+2y-10=0$ sont deux autres équations cartésiennes possibles de $(d)$.
Autre méthode possible avec le critère de colinéarité:
Soit $M(x;y)$ un point de la droite (d).
$\begin{cases} x_{\overrightarrow{AM}}=x_M-x_A=x-1 \\ y_{\overrightarrow{AM}}=y_M-y_A=y-2 \\ \end{cases}$
$\overrightarrow{AM}(x-1;y-2)$
$M\in$(d)
$\Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{AM}$ colinéaires
$\Longleftrightarrow x_{\overrightarrow{u}}y_{\overrightarrow{AM}}- y_{\overrightarrow{u}}x_{\overrightarrow{AM}}=0$
$\Longleftrightarrow -1(y-2)-3(x-1)=0$
$\Longleftrightarrow -y+2-3x+3=0$
$\Longleftrightarrow -3x-y+5=0$ - $A(2;0)$ et $\overrightarrow{u}(\sqrt{2};1-\sqrt{2})$
$\overrightarrow{u}(-b;a)$ est un vecteur directeur de la droite (d)Soit $M(x;y)$ un point de la droite (d).
$\begin{cases} x_{\overrightarrow{AM}}=x_M-x_A=x-2 \\ y_{\overrightarrow{AM}}=y_M-y_A=y \\ \end{cases}$
$\overrightarrow{AM}(x-2;y)$
$M\in (AB)$
$\Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{AM}$ colinéaires
$\Longleftrightarrow x_{\overrightarrow{u}}y_{\overrightarrow{AM}}- y_{\overrightarrow{u}}x_{\overrightarrow{AM}}=0$
$\Longleftrightarrow \sqrt{2}y-(1-\sqrt{2})(x-2)=0$
$\Longleftrightarrow \sqrt{2}y-(1-\sqrt{2})x+2-2\sqrt{2}=0$
$\Longleftrightarrow -(1-\sqrt{2})x+\sqrt{2}y+2-2\sqrt{2}=0$
$\Longleftrightarrow (-1+\sqrt{2})x+\sqrt{2}y+2-2\sqrt{2}=0$
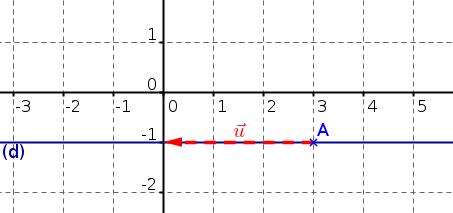
- $A(3;-1)$ et $\overrightarrow{u}(-3;0)$
$\overrightarrow{u}(-3;0)$ est un vecteur directeur de $(d)$
et si $ax+by+c=0$ est une équation cartésienne de $(d)$, le vecteur $\overrightarrow{u}(-b;a)$ est un vecteur directeur de $(d)$
donc ici $-b=-3$ soit $b=3$ et $a=0$ donc une équation cartésienne de $(d)$ est de la forme $0x+3y+c=0$
On peut utiliser les coordonnées du point $A$ pour calculer $c$:
$A\in (AB)\Longleftrightarrow 0x_A+3y_A+c=0\Longleftrightarrow 0\times 3+3\times (-1)+c=0\Longleftrightarrow c=3$
$\overrightarrow{u}(-3;0)$ donc $y_{\overrightarrow{u}}=0$
donc $(d)$ est parallèle à l'axe des abscisses
et $(d)$ admet une équation de la forme $y=$constante
soit $y=y_A=-1$
et $y=-1 \Longleftrightarrow y+1=0$
Donc $y+1=0$ est une équation cartésienne de $(AB)$
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 904
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Équation cartésienne d'une droite (rappels seconde)
- vecteur directeur
- équation cartésienne d'une droite
infos cours
| 10-15mn
série 2 : Équations cartésiennes (rappels seconde)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Équation cartésienne d'une droite
- rappels de seconde
- déterminer un vecteur directeur
- tracer une droite
- déterminer une équation cartésienne
infos: | 15mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.