Le plan est muni d'un repère orthonormé et on donne la droite $(d)$ d'équation $-3x+4y-6=0$
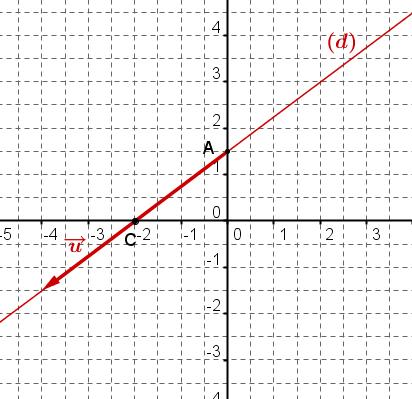
- Tracer $(d)$
Tracer une droite
Pour tracer une droite donnée par une équation cartésienne, on peut:
1. choisir deux valeurs de $x$ et calculer l'ordonnée correspondante avec l'équation de $(d)$ et placer les deux points obtenus
2. utiliser un vecteur directeur de $(d)$ et calculer l'ordonnée d'un point de $(d)$ en choisissant une valeur de $x$On peut aussi chercher $y$ lorsque $x=0$ puis utiliser le vecteur $ \overrightarrow{u}(-b;a)$ vecteur directeur de $(d)$.$ \overrightarrow{u}(-b;a)$ avec $a=-3$ (coefficient de $x$) et $b=4$ (coefficient de $y$) est un vecteur directeur de $(d)$
donc $ \overrightarrow{u}(-4;-3)$ est un vecteur directeur de $(d)$.
si $x=0$, on a : $-3\times 0+4y-6=0 \Longleftrightarrow y=\dfrac{6}{4} \Longleftrightarrow y=\dfrac{3}{2}$
- Déterminer les coordonnées du point d'intersection de $(d)$ et de l'axe des abscisses
Si on note $C$ ce point d'intersection, $C$ appartient à l'axe des abscisses donc son ordonnée $x_C=0$
$C\in (d)$ donc ses coordonnées vérifient une équation de $(d)$$C$ appartient à l'axe des abscisses donc $y_C=0$
$C\in (d)$ donc $-3x_C+4y_C-6=0$ avec $y_C=0$
$-3x_C-6=0 \Longleftrightarrow -3x_C=6$
$\phantom{-3x_C-6=0} \Longleftrightarrow x_C=\dfrac{6}{-3}$
$\phantom{-3x_C-6=0} \Longleftrightarrow x_C=-2$
On peut aussi présenter les calculs avec un système d'équations:
Une équation de l'axe des abscisses est $y=0$
Il faut donc résoudre:
$\begin{cases} y=0 \\ -3x+4y-6=0 \end{cases} \Longleftrightarrow \begin{cases} y=0 \\ -3x-6=0 \end{cases} \Longleftrightarrow \begin{cases} y=0 \\ x=-2 \end{cases}$ - Déterminer une équation cartésienne de $(d_1)$ perpendiculaire à $(d)$ puis tracer $(d_1)$
Vecteur normal
Le plan est muni d'un repère orthonormé.
Soit $(d)$ une droite, $\overrightarrow{n}$ est un vecteur normal à $(d)$ si $\overrightarrow{v}$ est orthogonal à tout vecteur directeur de $(d)$.
Si $ax+by+c=0$ est une équation cartésienne de $(d)$ alors$\overrightarrow{n}(a;b)$Le vecteur $ \overrightarrow{v}(a;b)$ avec $a=-3$ (coefficient de $x$) et $b=4$ (coefficient de $y$) est un vecteur normal à la droite $(d)$
donc $ \overrightarrow{v}(-3;4)$ est un vecteur normal à la droite $(d)$ donc un vecteur directeur de $(d_1)$
$(d_1)$ admet donc une équation cartésienne de la forme $-4x-3y+c=0$
$C(-2;0)\in (d_1) \Longleftrightarrow -4x_C-3y_C+c=0$
$\phantom{C(-2;0)\in (d_1)} \Longleftrightarrow -4\times (-2)-3\times 0+c=0$
$\phantom{C(-2;0)\in (d_1)} \Longleftrightarrow 8+c=0$
$\phantom{C(-2;0)\in (d_1)} \Longleftrightarrow c=-8$
En multipliant les deux membres par $-1$, on a aussi:
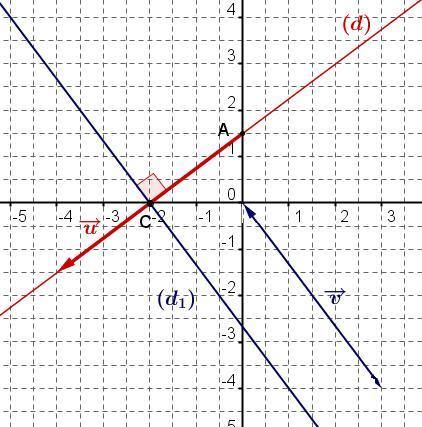
Pour tracer $(d_1)$ on peut utiliser le point $C$ et un vecteur directeur de $(d_1)$
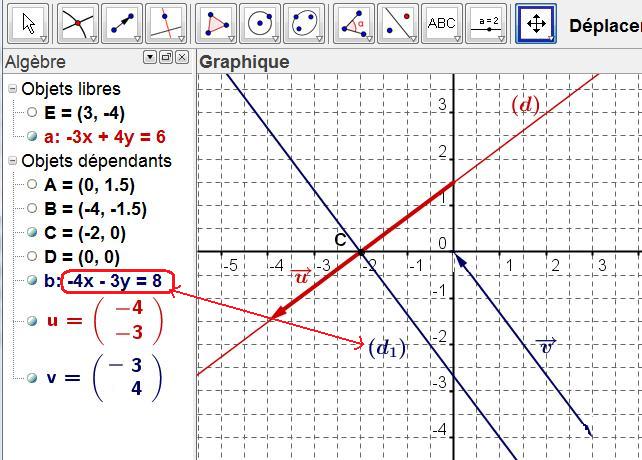
En utilisant GEOGEBRA et en traçant $(d)$ à partir de son équation cartésienne puis en plaçant le point C (commande: intersection) puis en traçant $(d_1)$ (commande: perpendiculaire à), on peut vérifier le calculs effectués.
- Déterminer une équation cartésienne de $(d_2)$ parallèle à $(d)$ passant par $D(4;0)$ puis la tracer.
$ \overrightarrow{u}(-4;-3)$ est un vecteur directeur de $(d)$ donc de $(d_2)$
Les coefficients de $x$ et $y$ dans une équations cartésienne de $(d_2)$ peuvent donc être identiques à ceux d'une équation cartésienne de $(d)$$ \overrightarrow{u}(-4;-3)$ est un vecteur directeur de $(d)$ donc de $(d_2)$
donc $(d_2)$ admet une équation de cartésienne de la forme $-3x+4y+c=0$
$D(4;0) \in (d_2)\Longleftrightarrow -3x_D+4y_D+c=0$
$\phantom{D(4;0) \in (d_2)}\Longleftrightarrow -12+0+c=0$
$\phantom{D(4;0) \in (d_2)}\Longleftrightarrow c=12$
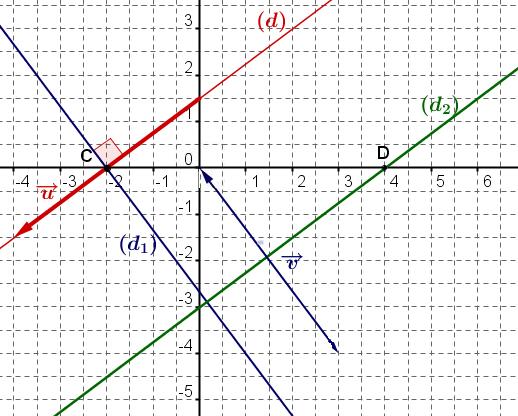
On peut aussi utiliser le critère de colinéarité pour déterminer une équation de $(d_2)$ (voir chapitre 5)
$M(x;y)\in (d_2) \Longleftrightarrow \overrightarrow{DM}$ et $ \overrightarrow{u}$ colinéaires
$\phantom{M(x;y)\in (d_2)} \Longleftrightarrow x_{ \overrightarrow{DM}} \times y_{ \overrightarrow{u}}-y_{ \overrightarrow{DM}} \times x_{ \overrightarrow{u}}=0$
$\phantom{M(x;y)\in (d_2)} \Longleftrightarrow (x_M-x_D) \times (-3)-(y_M-y_D)\times (-4)=0$
$\phantom{M(x;y)\in (d_2)} \Longleftrightarrow (x-4) \times (-3)-(y-0)\times (-4)=0$
$\phantom{M(x;y)\in (d_2)} \Longleftrightarrow -3x+12 +4y=0$
$\phantom{M(x;y)\in (d_2)} \Longleftrightarrow -3x+4y+12 =0$ - Que peut-on dire des droites $(d_1)$ et $d_2)$? Le vérifier par le calcul.
Vérifier qu'un vecteur directeur de $(d_1)$ et un vecteur directeur de $(d_2)$ sont orthogonaux.$(d_1)\perp (d)$ et $(d_2)//(d)$
donc $(d_1)\perp (d_2)$
(rappel: lorsque deux droites sont parallèles, toute perpendiculaire à l'une est aussi perpendiculaire à l'autre (propriété vue en sixième))
$ \overrightarrow{v}(-3;4)$ est un vecteur directeur de $(d_1)$
En reprenant le résultat précédent, $-3x+4y+12=0$est une équation cartésienne de $(d_2)$
donc $ \overrightarrow{w}(-4;-3)$ est un vecteur directeur de $(d_2)$
$ \overrightarrow{v}. \overrightarrow{w}=x_{ \overrightarrow{v}}\times x_{ \overrightarrow{w}}+y_{ \overrightarrow{v}}\times y_{ \overrightarrow{w}}=-3\times (-4)+4\times (-3)=0$
donc $ \overrightarrow{v}$ et $ \overrightarrow{w}$ sont orthogonaux
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 905
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Droites perpendiculaires
- vecteur normal
- équation cartésienne d'une perpendiculaire à une droite donnée
infos cours
| 10-15mn
série 3 : Droites perpendiculaires
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Droites perpendiculaires
- déterminer si deux droites sont perpendiculaires
- déterminer une équation cartésienne d'une perpendiculaire
infos: | mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.