Dans un jeu de 32 cartes, on tire une carte au hasard.
On marque 10 points si on tire un as, 5 points si on tire une carte de coeur (sauf l'as de coeur) et 0 point dans les autres cas.
Pour rappel, il y a 8 cartes de chaque couleur dans le jeu et il y a 4 as.
On note $X$ la variable aléatoire donnant le nombre de points obtenus à chaque tirage.
- Quelles sont les valeurs possibles pour $X$?
Variable aléatoire et loi de probabilité
Une variable aléatoire discrète est une fonction définie de $\Omega$ dans $\mathbb{R}$ qui a tout élément $x_i$ de $\Omega$ associe un nombre réel.
Définir la loi de probabilité d'une variable aléatoire prenant les valeurs $\left\lbrace x_1;x_2;x_3;......x_n\right\rbrace $, c'est déterminer la probabilité d'obtenir la valeur $X=x_i$ pour tout élément de $\left\lbrace x_1;x_2;x_3;......x_n\right\rbrace $$X$ correspond au nombre de points obtenus et le joueur marque 10, 5 ou 0 points
- Etablir la loi de probabilité de $X$.
Déterminer la probabilité correspondant à chaque cas.
Présenter les résultats dans un tableau.
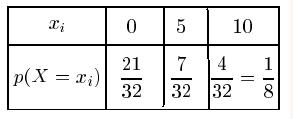
Rappel: dans un jeu de 32 cartes, il y a 4 as, 8 cartes de chaque couleur (coeur, trèfle, carreau et pique)La probabilité de marquer 10 points est la probabilité d'obtenir d'obtenir un as et vaut $\dfrac{4}{32}=\dfrac{1}{8}$
Il reste alors 7 cartes de coeur (huit moins l'as de coeur) donc la probabilité de marquer 5 points est de $\dfrac{7}{32}$
Pour marquer 0 point, il reste donc $32-4-7=21$ cartes possibles.
On a donc:
- Calculer alors l'espérance de la variable aléatoire $X$ et en donner la signification.
Espérance-variance-écart type
L'espérance de la variable aléatoire $X$ (avec les notations précédentes) est:
$E(X)=x_1p_1+x_2p_2+......+x_np_n=\sum_{i=1}^n p_ix_i$
La variance d'une variable aléatoire $X$ est:
$V(X)=p_1(x_1-E(X))^2+p_2(x_2-E(X))^2+.....+p_n(x_n-E(X))^2=\sum_{i=1}^n p_i(x_i-E(X))^2$
ou bien $V(X)=p_1x_1^2+p_2x_2^2+.....+p_nx_n^2-(E(X))^2=\sum_{i=1}^n p_ix_i^2-(E(X))^2$
L'écart type est égal à la racine carrée de la variance: $\sigma(X)=\sqrt{V(X)}$$E(X)=0\times \dfrac{21}{32}+5\times \dfrac{7}{32}+10\times \dfrac{4}{32}=\dfrac{75}{32}$
Cela signifie que pour un grand nombre de parties jouées, le joueur peut espérer gagner en moyenne 2,35 points par partie.
Attention les fonctions ci-dessous sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Cours nº 946
Vous pouvez retourner sur le cours après avoir vu cette vidéo.
Variables aléatoires
- variables aléatoires
- loi de probabilité
- espérance et écart type
- exemple
infos cours
| 15mn
série 4 : Variables aléatoires
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous emtraîner un peu plus, nous vous conseillons ces exercices.