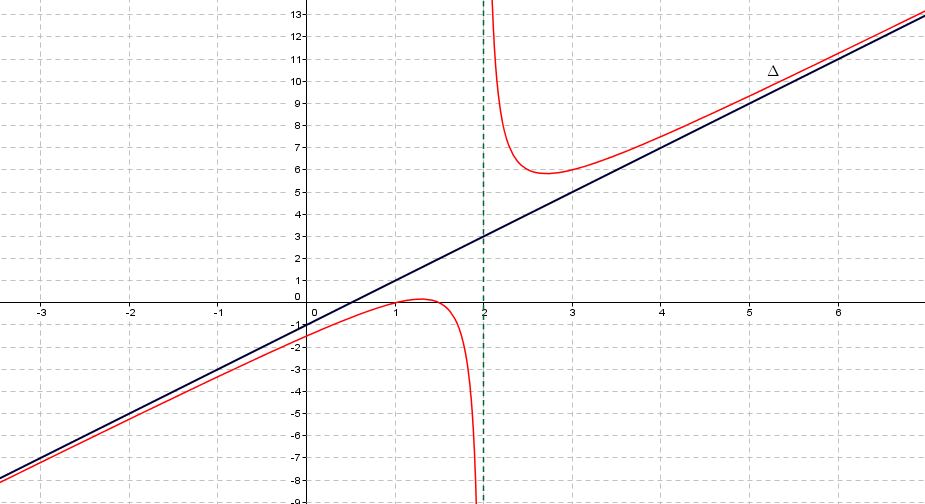
MATHS-LYCEELa fonction $f$ est définie sur $D_f=\mathbb{R}\setminus \lbrace 2\rbrace$ par $f(x)=\dfrac{2x^2-5x+3}{x-2}$ et on note $C_f$ sa représentation graphique dans un repère orthogonal.
- Déterminer les réels $a$ et $b$ tels que $f(x)=ax+b+\dfrac{1}{x-2}$ pour tout réel $x$ de $D_f$.
Il faut réduire au même dénominateur puis identifier les coefficients du numérateur pour qu'il soit égal à $2x^2-5x+3$Pour tout réel $x$ de $D_f$, on a:
$f(x)=ax+b+\dfrac{1}{x-2}$
$\phantom{f(x)}=\dfrac{(ax+b)(x-2)}{x-2}+\dfrac{1}{x-2}$
$\phantom{f(x)}=\dfrac{(ax+b)(x-2)+1}{x-2}$
$\phantom{f(x)}=\dfrac{ax^2+bx-2ax-2b+1}{x-2}$
et on a $f(x)=\dfrac{2x^2-5x+3}{x-2}$
donc par identification des coefficients au numérateur, on a:
$a=2$ (coefficient de $x^2$)
$b-2a=-5 \Longleftrightarrow b-4=-5 \Longleftrightarrow b=-1$ (coefficients de $x$)
On peut vérifier ensuite que $-2b+1=3$.
$-2\times (-1)+1=3$ (correct)
- Déterminer les limites de $f$ en $2$.
Opérations sur les limites
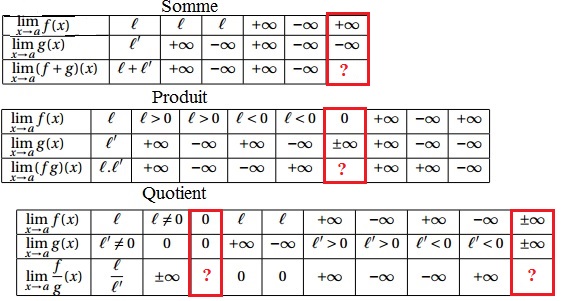Il faut d'abord chercher la limite de $x-2$ puis de $\dfrac{1}{x-2}$
Il faut distinguer les cas $x<2$ et $x>2$$\displaystyle \lim_{x \rightarrow 2}2x-1=2\times 2-1=3$
Cas $x <2$ soit $\displaystyle \lim_{x \rightarrow 2^-}f(x)$
$\displaystyle \lim_{x \rightarrow 2^-} x-2=0^-$ car $x-2<0$ pour $x< 2$
et par quotient $\displaystyle \lim_{x \rightarrow 2^-}\dfrac{1}{x-2}=-\infty$
Cas $x >2$ soit $\displaystyle \lim_{x \rightarrow 2^+}f(x)$
$\displaystyle \lim_{x \rightarrow 2^+} x-2=0^+$ car $x-2>0$ pour $x > 2$
et par quotient $\displaystyle \lim_{x \rightarrow 2^+}\dfrac{1}{x-2}=+\infty$
On peut en déduire que la droite d'équation $x=2$ est une asymptote à la courbe $C_f$. - Déterminer les limites de $f$ en $-\infty$ et $+\infty$
On peut chercher d'abord les limites de $2x-1$ et de $\dfrac{1}{x-2}$Limite en $-\infty$
$\displaystyle \lim_{x \rightarrow -\infty} 2x-1=-\infty$
$\displaystyle \lim_{x \rightarrow -\infty} x-2=-\infty$ et par quotient $\displaystyle \lim_{x \rightarrow -\infty}\dfrac{1}{x-2}=0$
Limite en $+\infty$
$\displaystyle \lim_{x \rightarrow +\infty} 2x-1=+\infty$
$\displaystyle \lim_{x \rightarrow +\infty} x-2=+\infty$ et par quotient $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x-2}=0$
- La droite $\Delta $ a pour équation $y=2x-1$.
Déterminer les limites en $+\infty$ et $-\infty$ de $f(x)-(2x-1)$.
Que peut-on en déduire pour la droite $\Delta$ et la courbe $C_f$ en $+\infty$ et $-\infty$?$f(x)-(2x-1)$ représente "l'écart" entre la droite $\Delta$ et la courbe $C_f$$f(x)-(2x-1)=2x-1+\dfrac{1}{x-2}-(2x-1)=\dfrac{1}{x-2}$
On peut reprendre les résultats de la question précédente soit:
$\displaystyle \lim_{x \rightarrow -\infty}\dfrac{1}{x-2}=0$ et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x-2}=0$
Cela signifie que la courbe $C_f$ et la droite $\Delta$ sont infiniment proches lorsque $x \longrightarrow +\infty$ et $x\longrightarrow -\infty$
- Compléter le tracé de $C_f$ ci-dessous.
devoir nº 1135
Vous pouvez retourner sur le devoir après avoir vu cet exercice
Devoir bilan limites
- limites et opérations sur les limites
- limites avec exponentielle et croissances comparées
- limites d'une fonction rationnelle et asymptotes
- asymptote oblique
infos cours
| 80mn