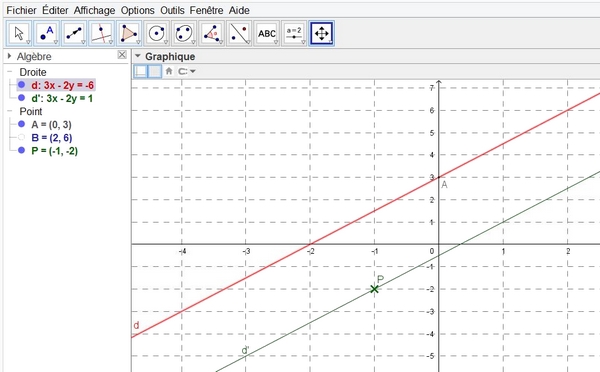
Dans le plan muni d'un repère orthogonal, on donne la droite $(d)$ d'équation $3x-2y+6=0$.
- Tracer $(d)$ dans un repère.
Vecteur directeur dans un repère
Dans un repère du plan, la droite $(d)$ a pour équation cartésienne $ax+by+c=0$ alors $\overrightarrow{u}(-b;a)$ est un vecteur directeur de $(d)$.
Si $(d)$ est définie par son équation réduite $y=ax+b$, $\overrightarrow{u}(1;a)$ est un vecteur directeur de $(d)$.
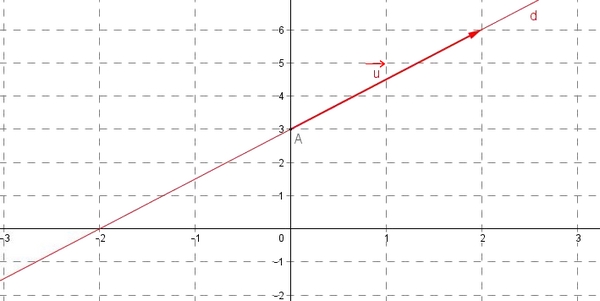
On peut utiliser un vecteur directeur de $(d)$ et les coordonnées d'un point $A$ de $(d)$ (à calculer)
Par exemple si $x_A=0$ calculer $y_A$On a ici $a=3$ et $b=-2$ donc $\overrightarrow{u}(2;3)$ est un vecteur directeur de $(d)$
Si $x=0$ alors on a $3\times 0-2y+6=0$
donc $y=\dfrac{-6}{-2}=3$
donc le point $A(0;3)$ appartient à $(d)$.
- Déterminer une équation cartésienne de la droite $(d')$ parallèle à $(d)$ et passant par $P(-1;-2)$
Droites parallèles
Deux droites parallèles ont des vecteurs directeurs colinéaires (ayant la même direction)Déterminer une équation cartésienne
Déterminer une équation cartésienne de la droite $(AB)$ avec $A(x_A;y_A)$ et $B(x_B;y_B)$ donnés dans un repère.
Méthode 1
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Si le point $M(x;y)$ appartient à $(AB)$, les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires
- $det(\overrightarrow{AM};\overrightarrow{AB})=0$
Méthode 2
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Les coordonnées de $\overrightarrow{AB}(-b;a)$ donnent les coefficients $a$ et $b$ d'une équation cartésienne
- $(AB)$: $ax+by+c=0$ et $A\in (AB)$ donc $ax_A+by_A+c=0$ (équation d'inconnue $c$)Un vecteur directeur de $(d)$ est aussi un vecteur directeur de $(d')$Rappel: $\overrightarrow{u}(2;3)$ est un vecteur directeur de $(d)$
Méthode 1
Soit $M(x;y)$ un point de $(d')$.
$\overrightarrow{PM}(x-(-1);y-(-2)$ soit $\overrightarrow{PM}(x+1;y+2$
$\overrightarrow{PM}$ et $\overrightarrow{u}$ colinéaires
$\Longleftrightarrow det(\overrightarrow{PM};\overrightarrow{u})=0$
$\Longleftrightarrow \begin{bmatrix} x+1&2\\ y+2&3\end{bmatrix}=0$
$\Longleftrightarrow 3(x+1)-2(y+2)=0$
$\Longleftrightarrow 3x+3-2y-4=0$
$\Longleftrightarrow 3x-2y-1=0$
Méthode 2:
$\overrightarrow{u}(2;3)$ est un vecteur directeur de $(d)$ donc de $(d')$.
$(d')$ admet une équation cartésienne de la forme $3x-2y+c'=0$
$P\in (d') \Longleftrightarrow 3x_P-2y_P+c'=0$
$~~~~~~~\Longleftrightarrow 3\times (-1)-2\times (-2)+c'=0$
$~~~~~~~\Longleftrightarrow -3+4+c'=0$
$~~~~~~~\Longleftrightarrow c'=-1$
- Contrôler les résultats en traçant les droites (avec GEOGEBRA par exemple)
devoir nº 436
Vous pouvez retourner sur le devoir après avoir vu cet exercice
Interrogation sur les équations cartésiennes (connaissances de base)
- équation cartésienne d'une droite passant par deux points
- équation cartésienne connaissant un point et un vecteur directeur
- équation cartésienne d'une parallèle
- intersection de deux droites et système d'équations
infos cours
| 20-30mn