1. Home
  2. chapitre 8 Équations de droites dans un repère
  3. exercice corrigé nº421
PDF reservé aux abonnés
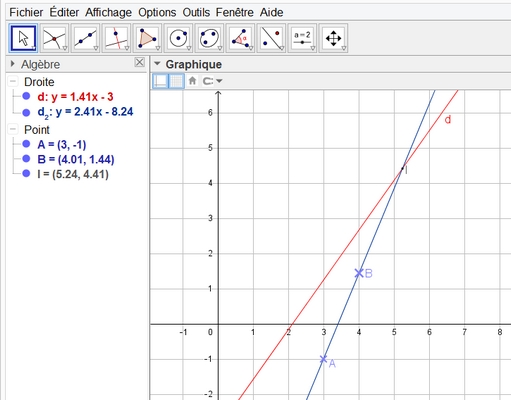
Dans le plan muni d'un repère orthogonal, la droite $d$ a pour équation réduite $y=\sqrt{2}x-3$ et on donne les points $A(3;-1)$ et $B(4;\sqrt{2})$.
  1. Déterminer l'équation réduite de $(AB)$.

    Rappel de cours

    Déterminer l'équation réduite de $(AB)$

    Dans un repère du plan, si $A(x_A;y_A)$ et $B(x_B;y_B)$ avec $x_A\neq x_B$, pour déterminer l'équation réduite de $(AB)$:
    - Calcul du coefficient directeur
    $a=\dfrac{\Delta_y}{\Delta_x}=\dfrac{y_B-y_A}{x_B-x_A}$
    - Calcul de $b$
    Le point $A$ appartient à la droite $(AB)$ donc ses coordonnées vérifient $y_A=ax_A+b$ (équation d'inconnue $b$)

    Solution

    $a=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{\sqrt{2}-(-1)}{4-3}=\sqrt{2}+1$
    L'équation réduite de $(AB)$ est de la forme $y=(\sqrt{2}+1)x+b$.
    $A(3;-1)$ appartient à la droite $(AB)$ donc $y_A=(\sqrt{2}+1)x_A+b$.
    $-1=(\sqrt{2}+1)\times 3+b \Longleftrightarrow -1=3\sqrt{2}+3+b$
    $\phantom{-1=(\sqrt{2}+1)\times 3+b} \Longleftrightarrow -1-3\sqrt{2}-3=b$
    $\phantom{-1=(\sqrt{2}+1)\times 2+b} \Longleftrightarrow -3\sqrt{2}-4=b$
  2. Déterminer les coordonnées du point d'intersection de $d$ et $(AB)$.

    Aide

    On doit résoudre le système d'équations formé avec les deux équations de droites
    Par substitution, il faut remplacer $y$ par son expression en fonction de $x$ dans la seconde équation

    Solution

    $d$ a pour équation réduite $y=\sqrt{2}x-3$.
    et $(AB)$ a pour équation réduite $y=(\sqrt{2}+1)x-3\sqrt{2}-4$
    donc il faut résoudre l'équation $\sqrt{2}x-3=(\sqrt{2}+1)x-3\sqrt{2}-4$
    $\sqrt{2}x-3=(\sqrt{2}+1)x-3\sqrt{2}-4 \Longleftrightarrow \sqrt{2}x-3=\sqrt{2}x+x-3\sqrt{2}-4$
    $\phantom{\sqrt{2}x-3=(\sqrt{2}+1)x-3\sqrt{2}-4} \Longleftrightarrow \sqrt{2}x-\sqrt{2}x-x=+3-3\sqrt{2}-4$
    $\phantom{\sqrt{2}x-3=(\sqrt{2}+1)x-3\sqrt{2}-4} \Longleftrightarrow -x=-3\sqrt{2}-1$
    $\phantom{\sqrt{2}x-3=(\sqrt{2}+1)x-3\sqrt{2}-4} \Longleftrightarrow x=3\sqrt{2}+1$
    et donc $y=\sqrt{2}\times (3\sqrt{2}+1)-3=3\times 2+\sqrt{2}-3=3+\sqrt{2}$.


    Contrôler rapidement avec la calculatrice en remplaçant $x$ par $3\sqrt{2}+1$ dans chacune des équations $y=\sqrt{2}x-3$ et $y=(\sqrt{2}+1)x-3\sqrt{2}-4$, on obtient bien $y_I=3+\sqrt{2}$
  3. Donner une valeur arrondie aux centièmes de $x_I$.
    Contrôler le résultat en traçant les deux droites avec un logiciel de géométrie(geogebra).

    Aide

    Avec Geogebra, il faut saisir les deux équations dans la barre de saisie (en bas d'écran)
    Avec Geogebra, la racine carrée de 2 s'écrit sqrt(2)

    Solution

    $x_I=3\sqrt{2}+1\approx 5,24$ et $y_I=3+\sqrt{2}\approx 4,41$

devoir nº 434


Vous pouvez retourner sur le devoir après avoir vu cet exercice

Devoir complet sur les équations réduites

- équation réduite d'une droite
- tracer une droite
- intersection de deux droites

infos cours

| 60mn

retour sur le devoir