Dans un jeu de 32 cartes, on tire une carte au hasard.
On marque 10 points si on tire un as, 5 points si on tire une carte de coeur (sauf l'as de coeur) et 0 point dans les autres cas.
Pour rappel, il y a 8 cartes de chaque couleur dans le jeu et il y a 4 as.
On note $X$ la variable aléatoire donnant le nombre de points obtenus à chaque tirage.
- Quelles sont les valeurs possibles pour $X$?
Variable aléatoire et loi de probabilité
Une variable aléatoire discrète est une fonction définie de $\Omega$ dans $\mathbb{R}$ qui a tout élément $x_i$ de $\Omega$ associe un nombre réel.
Définir la loi de probabilité d'une variable aléatoire prenant les valeurs $\left\lbrace x_1;x_2;x_3;......x_n\right\rbrace $, c'est déterminer la probabilité d'obtenir la valeur $X=x_i$ pour tout élément de $\left\lbrace x_1;x_2;x_3;......x_n\right\rbrace $$X$ correspond au nombre de points obtenus et le joueur marque 10, 5 ou 0 points
- Etablir la loi de probabilité de $X$.
Déterminer la probabilité correspondant à chaque cas.
Présenter les résultats dans un tableau.
Rappel: dans un jeu de 32 cartes, il y a 4 as, 8 cartes de chaque couleur (coeur, trèfle, carreau et pique)La probabilité de marquer 10 points est la probabilité d'obtenir d'obtenir un as et vaut $\dfrac{4}{32}=\dfrac{1}{8}$
Il reste alors 7 cartes de coeur (huit moins l'as de coeur) donc la probabilité de marquer 5 points est de $\dfrac{7}{32}$
Pour marquer 0 point, il reste donc $32-4-7=21$ cartes possibles.
On a donc:
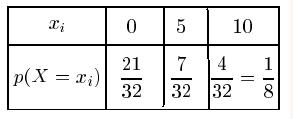
- Calculer alors l'espérance de la variable aléatoire $X$ et en donner la signification.
Espérance-variance-écart type
L'espérance de la variable aléatoire $X$ (avec les notations précédentes) est:
$E(X)=x_1p_1+x_2p_2+......+x_np_n=\sum_{i=1}^n p_ix_i$
La variance d'une variable aléatoire $X$ est:
$V(X)=p_1(x_1-E(X))^2+p_2(x_2-E(X))^2+.....+p_n(x_n-E(X))^2=\sum_{i=1}^n p_i(x_i-E(X))^2$
ou bien $V(X)=p_1x_1^2+p_2x_2^2+.....+p_nx_n^2-(E(X))^2=\sum_{i=1}^n p_ix_i^2-(E(X))^2$
L'écart type est égal à la racine carrée de la variance: $\sigma(X)=\sqrt{V(X)}$$E(X)=0\times \dfrac{21}{32}+5\times \dfrac{7}{32}+10\times \dfrac{4}{32}=\dfrac{75}{32}$
Cela signifie que pour un grand nombre de parties jouées, le joueur peut espérer gagner en moyenne 2,35 points par partie.
devoir nº 973
Vous pouvez retourner sur le devoir après avoir vu cet exercice
Calculs de probabilités avec un tableau à double entrée et espérance
- probabilités avec tableau à double entrée
- notations et calculs de probabilités et probabilités conditionnelles
- loi de probabilité d'une variable aléatoire
- espérance
infos cours
| 60mn