Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Le plan muni d'un repère orthonormé.
On donne les points $A(-3;2)$ et $B(3;4)$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On donne les points $A(-3;2)$ et $B(3;4)$.
- Placer les points $A$ et $B$ dans le repère puis déterminer une équation cartésienne de la droite $(AB)$
Déterminer une équation cartésienne
Déterminer une équation cartésienne de la droite $(AB)$ avec $A(x_A;y_A)$ et $B(x_B;y_B)$ donnés dans un repère.
Méthode 1
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Si le point $M(x;y)$ appartient à $(AB)$, les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires
- $det(\overrightarrow{AM};\overrightarrow{AB})=0$
Méthode 2
- calculer les coordonnée du vecteur $\overrightarrow{AB}$ vecteur directeur de $(AB)$
- Les coordonnées de $\overrightarrow{AB}(-b;a)$ donnent les coefficients $a$ et $b$ d'une équation cartésienne
- $(AB)$: $ax+by+c=0$ et $A\in (AB)$ donc $ax_A+by_A+c=0$ (équation d'inconnue $c$)
$\overrightarrow{AB}$ est un vecteur directeur de $(AB)$
$M \in (AB)$ si et seulement si A,B et M sont alignés.
$A$, B et M sont alignés si et seulement si $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires$\begin{cases} x_{\overrightarrow{AB}}=x_B-x_A=3-(-3)=6\\ y_{\overrightarrow{AB}}=y_B-y_A=4-2=2 \end{cases}$
donc $\overrightarrow{AB}(6;2)$
Soit $M(x;y)\in (AB)$ $\begin{cases} x_{\overrightarrow{AM}}=x_M-x_A=x-(-3)=x+3\\ y_{\overrightarrow{AM}}=y_M-y_A=y-2 \end{cases}$
donc $\overrightarrow{AM}(x+3;y-2)$
$M\in (AB)$
$\Longleftrightarrow x_{\overrightarrow{AM}}y_{\overrightarrow{AB}}-y_{\overrightarrow{AM}}x_{\overrightarrow{AB}}=0$
$\Longleftrightarrow (x+3)\times 2-(y-2)\times 6=0$
$\Longleftrightarrow 2x+6-6y+12=0$
$\Longleftrightarrow 2x-6y+18=0$
$\Longleftrightarrow x-3y+9=0$
On peut aussi utiliser les coordonnées de $\overrightarrow{AB}(6;2)$ pour obtenir les coefficients $a$ et $b$ de l'équation $ax+by+c=0$
$\overrightarrow{AB}(-b;a)$ est un vecteur directeur de $(AB)$ d'équation $ax+by+c=0$
donc $a=y_{\overrightarrow{AB}}=2$ et $b=-x_{\overrightarrow{AB}}=-6$
donc $(AB)$: $2x-6y+c=0$
$A(-3;2)\in (AB)$
$\Longleftrightarrow 2x_A-6y_A+c=0$
$\Longleftrightarrow -6-12+c=0$
$\Longleftrightarrow c=18$
donc une équation cartésienne de $(AB)$ est $2x-6y+18=0$
soit $x-3y+9=0$ - Déterminer une équation cartésienne de la droite $(d_1)$ passant par $B$ et de vecteur directeur $\overrightarrow{u}(1;-3)$ puis la tracer.
$M(x;y) \in (d_1)$ si et seulement $\overrightarrow{BM}$ et $\overrightarrow{u}$ sont colinéaires.
Soit $M(x;y)\in (d_1)$ $\begin{cases} x_{\overrightarrow{BM}}=x_M-x_B=x-3\\ y_{\overrightarrow{BM}}=y_M-y_B=y-4 \end{cases}$
donc $\overrightarrow{BM}(x-3;y-4)$
$M\in (d_1)$
$\Longleftrightarrow x_{\overrightarrow{BM}}y_{\overrightarrow{u}}-y_{\overrightarrow{BM}}x_{\overrightarrow{u}}=0$
$\Longleftrightarrow (x-3)\times (-3)-(y-4)\times 1=0$
$\Longleftrightarrow -3x+9-y+4=0$
$\Longleftrightarrow -3x-y+13=0$
On peut aussi utiliser les coordonnées de $\overrightarrow{u}(-1;3)$ pour obtenir les coefficients $a$ et $b$ de l'équation $ax+by+c=0$
$\overrightarrow{u}(-b;a)$ est un vecteur directeur de $(d_1)$ d'équation $ax+by+c=0$
donc $a=y_{\overrightarrow{u}}=3$ et $b=-x_{\overrightarrow{u}}=1$
donc $(AB)$: $3x+1y+c=0$
$B(3;4)\in (d_1)$
$\Longleftrightarrow 3x_B+y_B+c=0$
$\Longleftrightarrow 9+4+c=0$
$\Longleftrightarrow c=-13$
donc une équation cartésienne de $(d_1)$ est $3x+y-13=0$
- Soit $(d_2)$ d'équation $x+2y-1=0$.
Le point $A$ appartient-il à $(d_2)$?
Tracer $(d_2)$ dans le repère.Tracer une droite
Pour tracer une droite donnée par une équation cartésienne, on peut:
1. choisir deux valeurs de $x$ et calculer l'ordonnée correspondante avec l'équation de $(d)$ et placer les deux points obtenus
2. utiliser un vecteur directeur de $(d)$ et calculer l'ordonnée d'un point de $(d)$ en choisissant une valeur de $x$Un point appartient à une droite si ses coordonnées vérifient une équation de la droite
Pour tracer $(d_2)$, il faut déterminer les coordonnées de deux points de la droite
ou bien d'un point et d'un vecteur directeur$x_A+2y_A-1=-3+2\times 2-1=-3+-1=0$
$(d_2)$ a pour équation $x+2y-1=0$ donc $\overrightarrow{v}(-2;1)$ est un vecteur directeur de $(d_2)$ - Montrer que les droites $(d_2)$ et $(d_1)$ sont sécantes et calculer les coordonnées de leur point d'intersection $C$.
Deux droites sont sécantes si leurs vecteurs directeurs ne sont pas colinéaires (si les droites ne sont pas parallèles)
Pour trouver les coordonnées du point d'intersection de deux droites sécantes, il faut résoudre le système d'équations formé avec une équation de chacune d'elles$\overrightarrow{v}(-2;1)$ est un vecteur directeur de $(d_2)$ d'équation $x+2y-1=0$ et $\overrightarrow{u}(-1;3)$ est un vecteur directeur de $d_1)$
$x_{\overrightarrow{u}}y_{\overrightarrow{v}}-y_{\overrightarrow{u}}x_{\overrightarrow{v}}$
$=-1\times 1-3\times (-2)$
$=-1+6$
$=5\neq 0$
donc $\overrightarrow{u}$ et $\overrightarrow{v}$ ne sont pas colinéaires
donc $(d_1)$ et $(d_2)$ ne sont pas parallèles
Pour trouver les coordonnées du point d'intersection de ces deux droites, il faut résoudre le système d'équations formé avec une équation de chacune d'elles:
$\begin{cases} x+2y-1=0 \\ -3x-y+13=0 \end{cases}$
$\Longleftrightarrow \begin{cases} x=-2y+1 \\ -3(-2y+1)-y+13=0 \end{cases}$
$\Longleftrightarrow \begin{cases} x=-2y+1 \\ 6y-3-y+13=0 \end{cases}$
$\Longleftrightarrow \begin{cases} x=-2y+1 \\ 5y+10=0 \end{cases}$
$\Longleftrightarrow \begin{cases} x=-2y+1 \\ 5y=-10 \end{cases}$
$\Longleftrightarrow \begin{cases} x=-2\times (-2)+1=5 \\ y=\dfrac{-10}{5}=-2 \end{cases}$
- On note $I$ le milieu de $[AC]$.
Déterminer les coordonnées de $D$ symétrique de $B$ par rapport à $I$.Coordonnées du milieu d'un segment
Dans un repère du plan, si on a $A(x_A;y_A)$ et $B(x_B;y_B)$ alors le milieu $I$ de $[AB]$ a pour coordonnées $I\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)$on a $I$ milieu de $[BD]$ donc $x_I=\dfrac{x_B+x_D}{2}$ et $y_I=\dfrac{y_B+y_D}{2}$$I$ milieu de $[AC]$
$\begin{cases} x_I=\dfrac{x_A+x_C}{2}=\dfrac{-3+5}{2}=1 \\ y_I=\dfrac{y_A+y_C}{2}=\dfrac{2-2}{2}=0 \end{cases}$
$D$ symétrique de $B$ par rapport à $I$
$\Longleftrightarrow I$ milieu de $[BD]$
$\Longleftrightarrow \begin{cases} x_I=\dfrac{x_B+x_D}{2} \\ y_I=\dfrac{y_A+y_C}{2} \end{cases}$
$\Longleftrightarrow \begin{cases} 1=\dfrac{3+x_D}{2} \\ 0=\dfrac{4+y_C}{2} \end{cases}$
$\Longleftrightarrow \begin{cases} 2=3+x_D \\ 0=4+y_C \end{cases}$
$\Longleftrightarrow \begin{cases} -1=x_D \\ -4=y_C \end{cases}$
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
On peut aussi utiliser l'égalité vectorielle caractérisant le milieu de $[BD]$
$\overrightarrow{BI}=\overrightarrow{ID}$
$\Longleftrightarrow \begin{cases} x_I-x_B=x_D-x_I \\ y_I-y_B=y_D-y_I \end{cases}$
$\Longleftrightarrow \begin{cases} 1-3=x_D- 1 \\ 0-4=y_D-0 \end{cases}$
$\Longleftrightarrow \begin{cases} -1=x_D \\ -4=y_D \end{cases}$ - Calculer $AB$, $BC$ et $AC$ et en déduire la nature du quadrilatère $ABCD$
Distance dans un repère
Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$D'après la question 1, on a $\overrightarrow{AB}(6;2)$
donc $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{6^2+2^2}=\sqrt{40}$ unités
$BC=\sqrt{(x_C-x_B)^2+(y_C-y_B)^2}=\sqrt{(5-3)^2+(-2-4)^2}=\sqrt{40}$ unités
$AC=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}=\sqrt{(5-(-3))^2+(-2-2)^2}=\sqrt{80}$ unités L I milieu de [AC] et I milieu de [BD] donc les diagonales du quadrilatère ABCD se coupent en leurs milieux
$AB^2+BC^2=40+40=80$ et $AC^2=80$
donc $AB^2+BC^2=AC^2$ et $AB=BC$
donc le triangle ABC est un triangle rectangle isocèle en B
donc ABCD est un parallélogramme ayant un angle droit et deux côtés consécutifs de même longueur
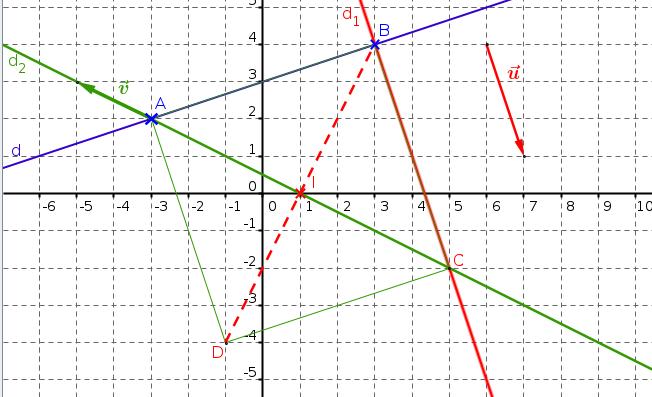
- Figure de l'exercice
Figure complète de l'exercice
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Équations cartésiennes
- tracer une droite définie par son équation cartésienne
- déterminer une équation cartésienne
- déterminer si deux droites sont parallèles
- déterminer une équation cartésienne d'une parallèle
infos: | 20-25mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
nº413 Vecteur directeur, intersection de deux droites
| 5-10mn |
nº429 Parallèles dans un parallélogramme
| 20-30mn |
nº1143 Bilan sur les équations de droites
| 15-20mn |
nº1601 Application des équations cartésiennes
| 8-12mn |
| 5-10mn |
nº429 Parallèles dans un parallélogramme
| 20-30mn |
nº1143 Bilan sur les équations de droites
| 15-20mn |
nº1601 Application des équations cartésiennes
| 8-12mn |
