Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
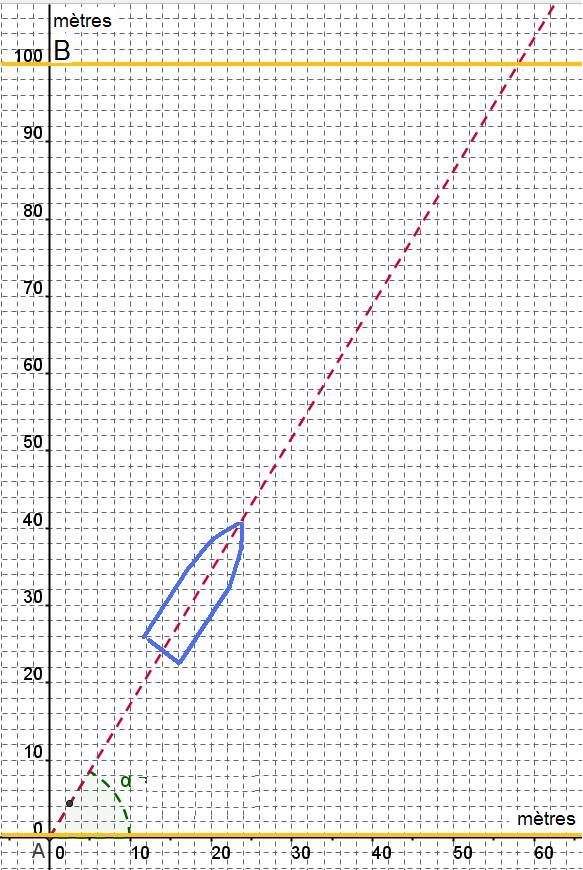
Un bateau traverse une rivière d'une largeur AB=100 mètres en partant du point A.
La vitesse du courant (vitesse de l'eau) est de $V_0=2 m s^{-1}$, ce courant de droite à gauche sur la figure et est parallèle aux berges symbolisées par l'axe des abscisses et la droite d'équation $y=100$ (tracées en jaune sur la figure) et la vitesse du bateau est $V_b=5 m s^{-1}$.
On note $\overrightarrow{v_b}$ le vecteur vitesse du bateau par rapport à l'eau (appelée route surface) et $\overrightarrow{v_0}$ le vecteur vitesse du courant.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
La vitesse du courant (vitesse de l'eau) est de $V_0=2 m s^{-1}$, ce courant de droite à gauche sur la figure et est parallèle aux berges symbolisées par l'axe des abscisses et la droite d'équation $y=100$ (tracées en jaune sur la figure) et la vitesse du bateau est $V_b=5 m s^{-1}$.
On note $\overrightarrow{v_b}$ le vecteur vitesse du bateau par rapport à l'eau (appelée route surface) et $\overrightarrow{v_0}$ le vecteur vitesse du courant.

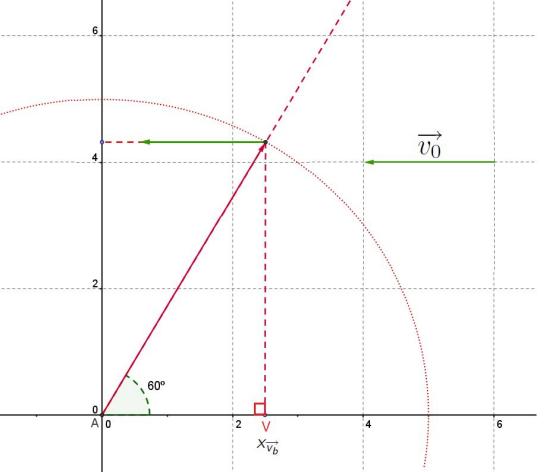
- Déterminer les coordonnées des vecteurs $\overrightarrow{v_0}$ et $\overrightarrow{v_b}$
$\overrightarrow{v_0}(-2;0)$
Dans le triangle AA'V rectangle en V, on a:
$cos(60^o)=\dfrac{\text{côté adjacent}}{\text{hypothénuse}}=\dfrac{AV}{AA'}=\dfrac{x_{\overrightarrow{v_b}}}{AA'}$
donc $x_{\overrightarrow{v_b}}=AA'\times cos(60^o)=\dfrac{5}{2}$
$sin(60^o)=\dfrac{\text{côté opposé}}{\text{hypothénuse}}=\dfrac{A'V}{AA'}=\dfrac{y_{\overrightarrow{v_b}}}{AA'}$
donc $y_{\overrightarrow{v_b}}=AA'\times sin(60^o)=\dfrac{5\sqrt{3}}{2}$
donc $\overrightarrow{v_b}\left(\dfrac{5}{2};\dfrac{5\sqrt{3}}{2} \right) $
- Construire le vecteur $\overrightarrow{v_R}$ correspondant au vecteur vitesse du bateau par rapport au fond (appelée route fond c'est à dire la vitesse et le déplacement réel par rapport à la terre).
Calculer ses coordonnées.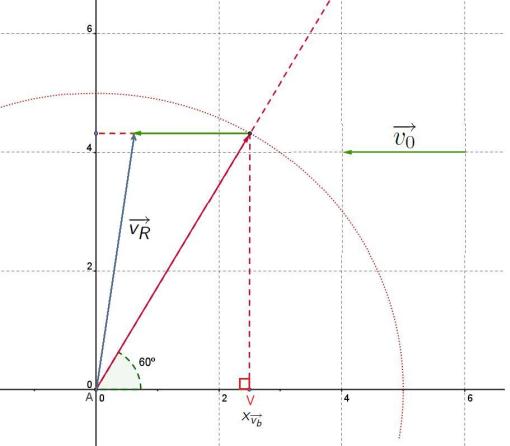
$\begin{cases} x_{\overrightarrow{v_R}}=x_{\overrightarrow{v_b}}+x_{\overrightarrow{v_0}}=\dfrac{5}{2}-2=\dfrac{1}{2}\\ y_{\overrightarrow{v_R}}=y_{\overrightarrow{v_b}}+y_{\overrightarrow{v_0}}=\dfrac{5\sqrt{3}}{2} \end{cases}$
donc $\overrightarrow{v_R}\left( \dfrac{1}{2}; \dfrac{5\sqrt{3}}{2}\right) $ - Déterminer une équation de la droite correspondant à la trajectoire du bateau et en déduire les coordonnées du point C où le bateau va accoster l'autre berge.
$\overrightarrow{v_R}$ est un vecteur directeur de cette droite$\overrightarrow{v_R}\left( \dfrac{1}{2}; \dfrac{5\sqrt{3}}{2}\right) $ est un vecteur directeur de la droite (d) correspondant à la trajectoire du bateau
Soit $M(x;y)$ un point de (d)
$\begin{cases} x_{\overrightarrow{AM}}=x_M-x_A=x \\ y_{\overrightarrow{AM}}=y_M-y_A=y \end{cases}$
donc $\overrightarrow{AM}(x;y)$
$M\in (d)$
$\Longleftrightarrow x_{v_R}y_{\overrightarrow{AM}}-y_{v_R}x_{\overrightarrow{AM}}=0$
$\Longleftrightarrow \dfrac{1}{2}y- \dfrac{5\sqrt{3}}{2}x=0$
$\Longleftrightarrow y-5\sqrt{3}x=0$ (on multiplie les deux membres par 2)
Le point C est le point d'intersection de (d) et de la droite d'équation $y=100$ donc $C(x_C;100)$
$C\in (d)$
$\Longleftrightarrow -5\sqrt{3}x_C+ 100=0$
$\Longleftrightarrow x_C=\dfrac{100}{5\sqrt{3}}$
$\Longleftrightarrow x_C=\dfrac{20}{\sqrt{3}}$
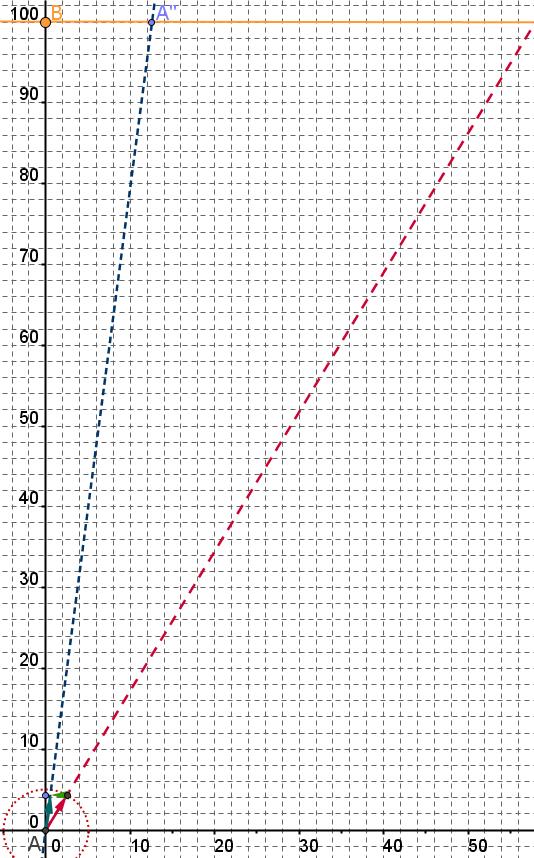
- On veut maintenant déterminer l'angle $\alpha $ que doit choisir le bateau pour arriver en B.
Exprimer les coordonnées du vecteur $\overrightarrow{v_b}$ puis du vecteur $\overrightarrow{v_R}$ en fonction de $cos(\alpha)$ et $sin(\alpha)$.
et en déduire la valeur de $\alpha$ arrondie au dixième de degréOn reprend la même méthode mais avec un angle $\alpha$ quelconque.
Dans le triangle AA'V rectangle en V, on a:
$cos(\alpha)=\dfrac{AV}{AA'}=\dfrac{x_{\overrightarrow{v_b}}}{AA'}$
donc $x_{\overrightarrow{v_b}}=AA'\times cos(\alpha )=5 cos(\alpha)$
$sin(\alpha)=\dfrac{A'V}{AA'}=\dfrac{y_{\overrightarrow{v_b}}}{AA'}$
donc $y_{\overrightarrow{v_b}}=AA'\times sin(\alpha)=\dfrac{sin(\alpha)}{2}$
$\begin{cases} x_{\overrightarrow{v_R}}=x_{\overrightarrow{v_b}}+x_{\overrightarrow{v_0}}=5 cos(\alpha)-2\\ y_{\overrightarrow{v_R}}=y_{\overrightarrow{v_b}}+y_{\overrightarrow{v_0}}=\dfrac{sin(\alpha)}{2} \end{cases}$
donc $\overrightarrow{v_R}\left( 5 cos(\alpha)-2; \dfrac{sin(\alpha)}{2}\right) $ Pour que la bateau arrive en B, il faut que $x_{v_R}=0$
donc il faut résoudre $5 cos(\alpha)-2=0$ $5 cos(\alpha)-2=0\Longleftrightarrow cos(\alpha)=\dfrac{2}{5}$
Avec la calculatrice (attention à régler les unités d'angle en degrés), on a $\alpha=cos^{-1}\left(\dfrac{2}{5} \right)\simeq 66,4$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Équations cartésiennes
- tracer une droite définie par son équation cartésienne
- déterminer une équation cartésienne
- déterminer si deux droites sont parallèles
- déterminer une équation cartésienne d'une parallèle
infos: | 20-25mn |
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
