Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
$ABCD$ est un carré et $M$ un point de $[BC]$.
On construit le triangle $BMN$ rectangle isocèle en $B$ extérieur au carré(voir figure).
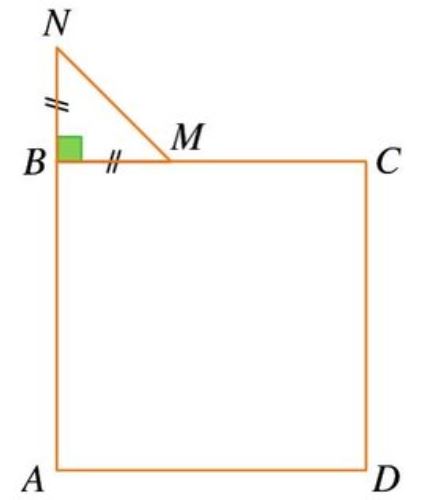
Montrer que les droites $(AM)$ et $(CN)$ sont perpendiculaires.
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non nuls, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On construit le triangle $BMN$ rectangle isocèle en $B$ extérieur au carré(voir figure).

Montrer que les droites $(AM)$ et $(CN)$ sont perpendiculaires.
Orthogonalité
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non nuls, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.
Il faut calculer le produit scalaire des vecteurs $\overrightarrow{AM}$ et $\overrightarrow{CN}$
On peut décomposer ces deux vecteurs avec la relation de Chasles.
On peut décomposer ces deux vecteurs avec la relation de Chasles.
$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}$
et $\overrightarrow{CN}=\overrightarrow{CB}+\overrightarrow{BN}$
$\overrightarrow{AM}.\overrightarrow{CN}$
$=(\overrightarrow{AB}+\overrightarrow{BM}).(\overrightarrow{CB}+\overrightarrow{BN})$
$=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{BM}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BN}+\overrightarrow{BM}.\overrightarrow{BN}$
$ABCD$ est un carré et $M\in [BC]$ et $N\in (AB)$
donc $\overrightarrow{AB}$ et $\overrightarrow{CB}$ sont orthogonaux et $\overrightarrow{AB}.\overrightarrow{CB}=0$
De plus $\overrightarrow{BM}$ et $\overrightarrow{BN}$ sont orthogonaux donc $\overrightarrow{BM}.\overrightarrow{BN}=0$
$\overrightarrow{BM}$ et $\overrightarrow{CB}$ sont colinéaires et de sens contraires
donc $\overrightarrow{BM}.\overrightarrow{CB}=BM\times CB\times cos(\pi)=-BM\times CB$
$ \overrightarrow{AB}$ et $\overrightarrow{BN}$ sont colinéaires et de même sens
donc $\overrightarrow{AB}.\overrightarrow{BN}=AB\times BN\times cos(0)=AB\times BN$
On a donc:
$\overrightarrow{AM}.\overrightarrow{CN}$
$=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{BM}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BN}+\overrightarrow{BM}.\overrightarrow{BN}$
$=0-BM\times CB+AB\times BN+0$
$=-BN\times AB+AB\times BN$ car $AB=CB$ et $BN=BM$
$=0$
donc $\overrightarrow{AM}$ et $\overrightarrow{CN}$ sont orthogonaux
et $\overrightarrow{CN}=\overrightarrow{CB}+\overrightarrow{BN}$
$\overrightarrow{AM}.\overrightarrow{CN}$
$=(\overrightarrow{AB}+\overrightarrow{BM}).(\overrightarrow{CB}+\overrightarrow{BN})$
$=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{BM}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BN}+\overrightarrow{BM}.\overrightarrow{BN}$
$ABCD$ est un carré et $M\in [BC]$ et $N\in (AB)$
donc $\overrightarrow{AB}$ et $\overrightarrow{CB}$ sont orthogonaux et $\overrightarrow{AB}.\overrightarrow{CB}=0$
De plus $\overrightarrow{BM}$ et $\overrightarrow{BN}$ sont orthogonaux donc $\overrightarrow{BM}.\overrightarrow{BN}=0$
$\overrightarrow{BM}$ et $\overrightarrow{CB}$ sont colinéaires et de sens contraires
donc $\overrightarrow{BM}.\overrightarrow{CB}=BM\times CB\times cos(\pi)=-BM\times CB$
$ \overrightarrow{AB}$ et $\overrightarrow{BN}$ sont colinéaires et de même sens
donc $\overrightarrow{AB}.\overrightarrow{BN}=AB\times BN\times cos(0)=AB\times BN$
On a donc:
$\overrightarrow{AM}.\overrightarrow{CN}$
$=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{BM}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BN}+\overrightarrow{BM}.\overrightarrow{BN}$
$=0-BM\times CB+AB\times BN+0$
$=-BN\times AB+AB\times BN$ car $AB=CB$ et $BN=BM$
$=0$
donc $\overrightarrow{AM}$ et $\overrightarrow{CN}$ sont orthogonaux
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
