Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
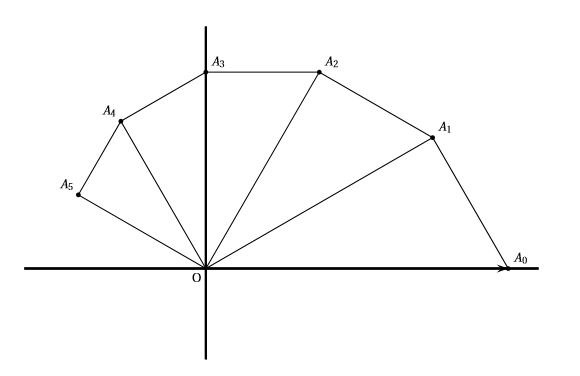
Le plan complexe est muni d'un repère orthonormé $(O;\overrightarrow{i};\overrightarrow{j})$.
Pour tout entier naturel $n$, on note $A_{n}$ le point d'affixe $z_{n}$ défini par : $z_{0} = 1$ et $ z_{n+1} = \left(\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i\right)z_{n}$.
On définit la suite $\left(r_{n}\right)$ par $r_{n} = \left|z_{n}\right|$ pour tout entier naturel $n$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Pour tout entier naturel $n$, on note $A_{n}$ le point d'affixe $z_{n}$ défini par : $z_{0} = 1$ et $ z_{n+1} = \left(\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i\right)z_{n}$.
On définit la suite $\left(r_{n}\right)$ par $r_{n} = \left|z_{n}\right|$ pour tout entier naturel $n$.
- Donner la forme exponentielle du nombre complexe $\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i$.
Forme trigonométrique
Soit $z=x+iY$ un complexe.
Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
Cette forme est appelée forme trigonométrique} de $z$.Forme exponentielle
$z$ est un complexe d'argument $\alpha$
La forme exponentielle de $z$ est $z=|z|e^{i\alpha}$$\left\vert \dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i\right\vert=\sqrt{\left(\dfrac{3}{4}\right)^2+\left(\dfrac{\sqrt{3}}{4}\right)^2}=\sqrt{\dfrac{12}{16}}=\dfrac{\sqrt{12}}{4}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}$
$\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i=\dfrac{\sqrt{3}}{2}\left(\dfrac{2}{\sqrt{3}}\times \dfrac{3}{4}+i\dfrac{2}{\sqrt{3}}\times \dfrac{\sqrt{3}}{4}\right)=\dfrac{\sqrt{3}}{2}\left(\dfrac{3}{2\sqrt{3}}+i\dfrac{1}{2}\right)$
En posant $\theta=arg\left(\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i\right)$, on a donc le système d'équations suivant:
$\begin{cases} cos(\theta)=\dfrac{3}{2\sqrt{3}}\\ sin(\theta)=\dfrac{1}{2} \end{cases} \Longleftrightarrow \begin{cases} cos(\theta)=\dfrac{3\sqrt{3}}{2\sqrt{3}\sqrt{3}}\\ sin(\theta)=\dfrac{1}{2} \end{cases} \Longleftrightarrow \begin{cases} cos(\theta)=\dfrac{\sqrt{3}}{2}\\ sin(\theta)=\dfrac{1}{2} \end{cases}$ donc $\theta=\dfrac{\pi}{6}$ ($2\pi$)
-
- Montrer que la suite $\left(r_{n}\right)$ est géométrique de raison $\dfrac{\sqrt{3}}{2}$.
Suite géométrique
Une suite $(u_n)$ est géométrique s'il existe un réel $q$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n\times q$
$q$ est la raison de la suite.
Le quotient de deux termes consécutifs est égal à la raison soit $\dfrac{u_{n+1}}{u_n}=q$Il faut montrer que $r_{n+1}=qr_n$ et $r_{n+1}=|z_{n+1}|$Pour tout entier naturel $n$ on a:
$r_{n+1}=|z_{n+1}|$ et $ z_{n+1} = \left(\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i\right)z_{n}$
$\phantom{r_{n+1}}=\left\vert\left(\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i\right)z_{n}\right\vert$
$\phantom{r_{n+1}}=\left\vert\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}\right\vert \left\vert z_{n}\right\vert$ et $\left\vert\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}\right\vert=\dfrac{\sqrt{3}}{2}$
$\phantom{r_{n+1}}=\dfrac{\sqrt{3}}{2} \left\vert z_{n}\right\vert$
$\phantom{r_{n+1}}=\dfrac{3\sqrt{2}}{4} r_n$
- En déduire l'expression de $r_{n}$ en fonction de $n$.
Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$Une suite géométrique est définie par sa raison et son premier terme
$r_n=|z_n|$ et donc $r_0=|z_0|$$r_0=|z_0|=|1|=1$
- Que dire de la longueur $OA_{n}$ lorsque $n$ tend vers $+ \infty$ ?
Limite de $q^n$ (suite géométrique)
Si $q > 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=+\infty$
Si $-1 < q < 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=0$$OA_n=|z_n|=r_n$On a $q=\dfrac{\sqrt{3}}{2}$ donc $q\in]-1;1[$
donc $\displaystyle \lim_{n \rightarrow +\infty}r_n=0$
$A_n$ a pour affixe $z_n$ donc $OA_n=|z_n|=r_n$
- Montrer que la suite $\left(r_{n}\right)$ est géométrique de raison $\dfrac{\sqrt{3}}{2}$.
- On considère l'algorithme suivant :
- Quelle est la valeur affichée par l'algorithme pour $P = 0,5$ ?
A chaque passage dans la boucle TANT QUE, on ajoute 1 à l'indice $n$ et on calcule le terme suivant de la suite $(r_n)$ soit $\dfrac{\sqrt{3}}{2}r_n$On peut consigner les résultats dans un tableau:
\begin{tabular}{|c|c|c|c|c|c|c|c|} \hline Test&&vrai&vrai&vrai&vrai&vrai&faux\\ \hline Valeur de $n$&0&1&2&3&4&5&5\\ \hline Valeur de R&1&$\dfrac{\sqrt{3}}{2}$&$\dfrac{3}{4}$&$\dfrac{3\sqrt{3}}{8}$&$\dfrac{9}{16}$&$\dfrac{9\sqrt{3}}{32}$&$\dfrac{9\sqrt{3}}{32}$\\ \hline \end{tabular}
L'algorithme affiche donc la première valeur de $n$ pour laquelle $r_n> 0,5$ - Pour $P = 0,01$ on obtient $n = 33$.
Quel est le rôle de cet algorithme ?On recherche donc à partir de quel indice la distance $OA_n$ soit $r_n=|z_n|$ est inférieure à $P=0,01$TANT QUE $r_n > 0,01$ alors on effectue le passage dans la boucle TANT QUE.
Le rôle de l'algorithme est donc de déterminer à partir de quel indice la distance $OA_n$ est inférieure ou égale à 0,01
- Quelle est la valeur affichée par l'algorithme pour $P = 0,5$ ?
-
- Démontrer que le triangle $OA_{n}A_{n+1}$ est rectangle en $A_{n+1}$.
On peut calculer les distances $OA_{n+1}$, $OA_n$ et $A_nA_{n+1}$ en utilisant les modules de $z_n$, $z_{n+1}$ et de $z_{n+1}-z_n$$OA_{n+1}=r_{n+1}=\dfrac{\sqrt{3}}{2}r_n$
$OA_n=r_n$
$A_nA_{n+1}=\left\vert z_{n+1}-z_n\right\vert$
$\phantom{A_nA_{n+1}}=\left\vert \left(\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}i\right)z_{n}-z_n\right\vert$
$\phantom{A_nA_{n+1}}=\left\vert \left(\dfrac{3}{4}-1 + \dfrac{\sqrt{3}}{4}i\right)z_{n}\right\vert$
$\phantom{A_nA_{n+1}}=\left\vert \left(\dfrac{-1}{4} + \dfrac{\sqrt{3}}{4}i\right)z_{n}\right\vert$
$\phantom{A_nA_{n+1}}=\left\vert \dfrac{-1}{4} + \dfrac{\sqrt{3}}{4}i\right\vert \times \left\vert z_{n}\right\vert$
$\phantom{A_nA_{n+1}}=\sqrt{\left(\dfrac{-1}{4}\right)^2 + \left(\dfrac{\sqrt{3}}{4}\right)^2} \times r_n$
$\phantom{A_nA_{n+1}}=\sqrt{\dfrac{4}{16}} \times r_n$
$\phantom{A_nA_{n+1}}=\dfrac{1}{2}r_n$
$OA_{n+1}^2+A_nA_{n+1}^2=\left(\dfrac{\sqrt{3}}{2}r_n\right)^2+\left(\dfrac{1}{2}r_n\right)^2$
$\phantom{OA_{n+1}^2+A_nA_{n+1}^2}=\dfrac{3}{4}r_n^2+\dfrac{1}{4}r_n^2$
$\phantom{OA_{n+1}^2+A_nA_{n+1}^2}=r_n^2$
$\phantom{OA_{n+1}^2+A_nA_{n+1}^2}=OA_n^2$
- On admet que $z_{n} = r_{n}e^{i\frac{n\pi}{6}}$.
Déterminer les valeurs de $n$ pour lesquelles $A_{n}$ est un point de l'axe des ordonnées.$A_n$ appartient à l'axe des ordonnées si sa partie réelle est nulle donc si l'argument de $z_n$ est $\dfrac{\pi}{2}$ ($2\pi$) ou bien $\dfrac{-\pi}{2}$ ($2\pi$)$A_n$ appartient à l'axe des ordonnées si sa partie réelle est nulle donc si l'argument de $z_n$ est $\dfrac{\pi}{2}$ ($2\pi$) ou bien $\dfrac{-\pi}{2}$ ($2\pi$)
donc on doit avoir $arg(z_n)=\dfrac{\pi}{2}+k\pi$ avec $k\in \mathbb{Z}$
or $arg(z_n)=\dfrac{n\pi}{6}$ ($2\pi$)
donc $\dfrac{n\pi}{6}=\dfrac{\pi}{2}+k\pi$ avec $k\in \mathbb{Z}$
$\dfrac{n\pi}{6}=\dfrac{\pi}{2}+k\pi \Longleftrightarrow \dfrac{n}{6}=\dfrac{1}{2}+k \Longleftrightarrow n=3+6k$
On a $n \in \mathbb{N}$ donc $k\in \mathbb{N}$
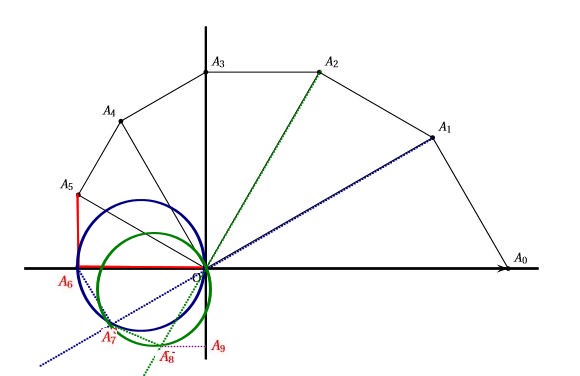
- Compléter la figure donnée ci-dessous en représentant les points $A_{6}, A_{7}, A_{8}$ et $A_{9}$.
Les traits de construction seront apparents.
On sait que le triangle $OA_5A_6$ est rectangle en $A_6$ et $z_6=r_6e^{i\frac{6\pi}{6}e_6e^{i\pi}$$z_6=r_6e^{i\frac{6\pi}{6}}=r_6e^{i\pi}=r_6\left(cos(\pi)+isin(\pi)\right)=-r_6$ (rappel $sin(\pi)=0$)
donc $A_6$ appartient à l'axe des abscisses.
$arg(z_1)=\dfrac{\pi}{6}$ ($2\pi$) et $arg(z_7)=\dfrac{7\pi}{6}=\pi+\dfrac{\pi}{6}$ ($2\pi$)
donc les points $A_1$, $O$ et $A_7$ sont alignés et $OA_6A_7$ est un triangle rectangle en $A_7$ ($A_7$ appartient donc au cercle de diamètre $[OA_6]$.
De même $A_8$ est aligné avec $O$ et $A_2$ et $A_8$ appartient au cercle de diamètre $[OA_7]$.
Si $k=1$ alors $n=3+6=9$ et donc $A_9$ appartient à l'axe des ordonnées.
- Démontrer que le triangle $OA_{n}A_{n+1}$ est rectangle en $A_{n+1}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)