Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On considère la suite de nombres complexes $\left(z_n\right)$ définie par $z_0=\sqrt{3}-i$ et pour tout entier naturel $n$: $z_{n+1} = (1+i)z_n$.
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Pour tout entier naturel $n$, on pose $u_n = \left|z_{n}\right|$.
Partie B
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
Pour tout entier naturel $n$, on pose $u_n = \left|z_{n}\right|$.
- Calculer $u_0$.
Forme trigonométrique
Soit $z=x+iY$ un complexe.
Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
Cette forme est appelée forme trigonométrique} de $z$.$u_0=|z_0|=|\sqrt{3}-i|=\sqrt{\sqrt{3}^2+(-1)^2}=\sqrt{3+1}=2$
- Démontrer que $\left(u_n\right)$ est la suite géométrique de raison $\sqrt{2}$.
Suite géométrique
Une suite $(u_n)$ est géométrique s'il existe un réel $q$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n\times q$
$q$ est la raison de la suite.
Le quotient de deux termes consécutifs est égal à la raison soit $\dfrac{u_{n+1}}{u_n}=q$On veut montrer que $u_{n+1}=qu_n$
$u_{n+1}= |z_{n+1}| = |(1+i)z_n|=|1+i||z_n|$Pour tout entier naturel $n$ on a:
$u_{n+1}= |z_{n+1}|$
$\phantom{u_{n+1}} = |(1+i)z_n|$
$\phantom{u_{n+1}}=|1+i||z_n|$
$\phantom{u_{n+1}}=\sqrt{1^2+1^2}|z_n|$
$\phantom{u_{n+1}}=\sqrt{2}|z_n|$
$\phantom{u_{n+1}}=\sqrt{2}u_n$
- Pour tout entier naturel $n$, exprimer $u_n$ en fonction de $n$.
Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$$(u_n)$ est une suite géométrique de raison $q=\sqrt{2}$ et de premier terme $u_0=2$
- Déterminer la limite de la suite $\left(u_n\right)$.
Limite de $q^n$ (suite géométrique)
Si $q > 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=+\infty$
Si $-1 < q < 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=0$La raison est ici $\sqrt{2}>1$ et $u_0>0$La raison de la suite $(u_n)$ est $q=\sqrt{2}$ donc $q>1$
et on a $u_0 >0$
- Étant donné un réel positif $p$, on souhaite déterminer, à l'aide d'un algorithme, la plus petite valeur de l'entier naturel $n$ telle que $u_n > p$.
Recopier l'algorithme ci-dessous et le compléter par les instructions de traitement et de sortie, de façon à afficher la valeur cherchée de l'entier $n$.
On veut à chaque passage dans la boucle TANT QUE calculerle terme suivant pour la suite et augmenter l'indice de 1$n$ représente les indices successifs et $u$ la valeur de chaque terme de la suite.
A chaque passage dans la boucle, on veut donc $n+1\longrightarrow n$ et $\sqrt{2}u\longrightarrow u$.
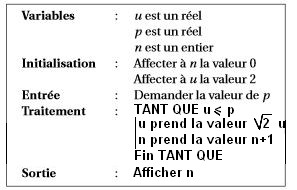
Partie B
- Déterminer la forme algébrique de $z_1$.
$z_0=\sqrt{3}-i$ et $z_{1} = (1+i)z_0$
$z_1=(1+i)(\sqrt{3}-i)=\sqrt{3}-i+i\sqrt{3}-i^2=\sqrt{3}+1+i(\sqrt{3}-1)$
- Déterminer la forme exponentielle de $z_0$ et de $1+i$.
En déduire la forme exponentielle de $z_1$.Forme trigonométrique
Soit $z=x+iY$ un complexe.
Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
Cette forme est appelée forme trigonométrique} de $z$.Forme exponentielle
$z$ est un complexe d'argument $\alpha$
La forme exponentielle de $z$ est $z=|z|e^{i\alpha}$Il faut calculer $|z_0|$ et $|1+i|$
On utilise ensuite $e^{i\alpha}e^{i\theta}=e^{i(\alpha+\theta)}$$z_0=\sqrt{3}-i$
$|z_0|=\sqrt{\sqrt{3}^2+(-1)^2}=\sqrt{3+1}=2$
$z_0=2\left(\dfrac{\sqrt{3}}{2}-i\dfrac{1}{2}\right)$
Si on note $\alpha=arg(z_0)$ ($2\pi$) on a alors $\begin{cases}cos(\alpha)=\dfrac{\sqrt{3}}{2}\\ sin(\alpha)=\dfrac{-1}{2} \end{cases}$
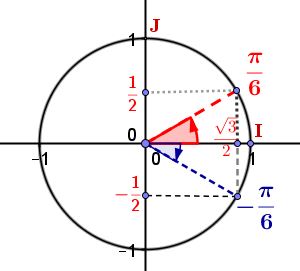
donc $arg(z_1)=\dfrac{-\pi}{6}$ ($2\pi$)
$|1+i|=\sqrt{1^2+1^2}=\sqrt{2}$
$1+i=\sqrt{2}\left(\dfrac{1}{\sqrt{2}}+i\dfrac{1}{\sqrt{2}}\right)$
Si on note $\theta=arg(1+i)$ ($2\pi$) on a alors $\begin{cases}cos(\alpha)=\dfrac{1}{\sqrt{2}}\\ sin(\alpha)=\dfrac{1}{\sqrt{2}} \end{cases} \Longleftrightarrow \begin{cases}cos(\alpha)=\dfrac{\sqrt{2}}{2}\\ sin(\alpha)=\dfrac{\sqrt{2}}{2} \end{cases}$
donc $arg(1+i)=\dfrac{\pi}{4}$ ($2\pi$)
$z_1=(1+i)z_0=\sqrt{2}e^{i\frac{\pi}{4}}\times 2e^{-i\frac{\pi}{6}}=2\sqrt{2} e^{i\left(\frac{\pi}{4}-\frac{\pi}{6}\right)}=2\sqrt{2} e^{i\frac{\pi}{12}}$
- Déduire des questions précédentes la valeur exacte de $\cos\left(\dfrac{\pi}{12}\right)$
Deux complexes sont égaux si leurs parties réelles et imaginaires sont égales
Il faut donc utiliser les deux formes d'écriture de $z_1$: algébrique et trigonométrique$z_1=2\sqrt{2} e^{i\frac{\pi}{12}}=2\sqrt{2}\left(cos\left(\dfrac{\pi}{12}\right)+isin\left(\dfrac{\pi}{12}\right)\right)$
et on a $z_1=\sqrt{3}+1+i(\sqrt{3}-1)$
donc $2\sqrt{2}cos\left(\dfrac{\pi}{12}\right)=\sqrt{3}+1$
soit $cos\left(\dfrac{\pi}{12}\right)=\dfrac{\sqrt{3}+1}{2\sqrt{2}}=\dfrac{(\sqrt{3}+1)\sqrt{2}}{2\sqrt{2}\sqrt{2}}=\dfrac{\sqrt{6}+\sqrt{2}}{4}$
Le dernier calcul n'est pas indispensable car on ne demande pas d'écrire le résultat sans racine carrée au dénominateur.
Penser à contrôler le résultat avec la calculatrice en calculant d'une part $cos\left(\dfrac{\pi}{12}\right)$ et $\dfrac{\sqrt{6}+\sqrt{2}}{4}$ d'autre part.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)