MATHS-LYCEE.FR exercice corrigé chapitre Produit scalaire

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)

PDF reservé aux abonnés

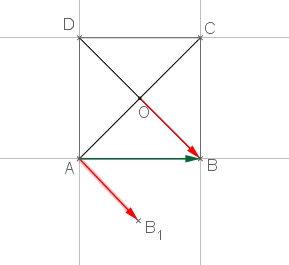
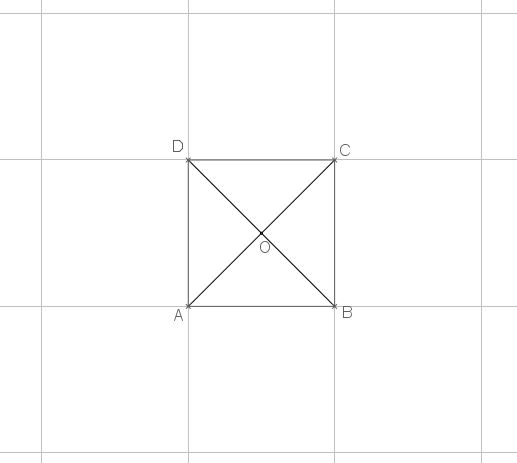
$ABCD$ est un carré de centre $O$ et de côté $a$.

Calculer $\overrightarrow{CD}. \overrightarrow{CA}$.

Rappel de cours

Produit scalaire et projeté orthogonal
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)

Aide

On peut utiliser le projeté orthogonal de $A$ sur $(CD)$

Solution

On a les deux vecteurs suivants de même origine:

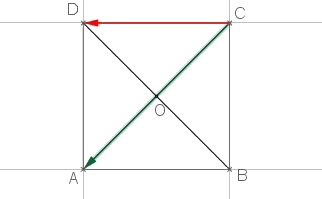
Le projeté orthogonal de $A$ sur $(CD)$ est le point $H$ confondu avec $D$.

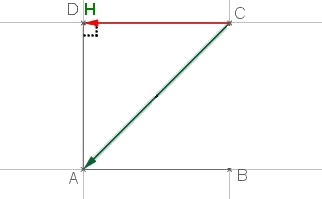
On a aussi $\overrightarrow{CD}.\overrightarrow{CA}=CD\times CA \times cos(\widehat{ACD})=a\times \sqrt{2}a\times cos\left(\dfrac{\pi}{4}\right)=\sqrt{2}a^2\times \dfrac{\sqrt{2}}{2}=a^2$ Pour calculer $AC$, on utilise le théorème de Pythagore dans le triangle $ACD$.
Calculer $\overrightarrow{AD}. \overrightarrow{CB}$.

Rappel de cours

Produit scalaire et projeté orthogonal
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
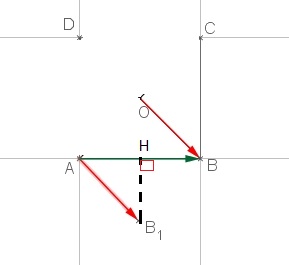
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)

Aide

On peut utiliser le projeté orthogonal de $D$ sur $(BC)$

Solution

On a les deux vecteurs suivants de même origine avec $\overrightarrow{AB_1}=\overrightarrow{CD}$ (en vert)

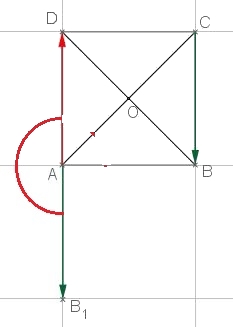
$\overrightarrow{AD}. \overrightarrow{CB}$
$=AD\times CB \times cos(\widehat{B_1AD})$
$=a^2 \times cos(\widehat{\pi})$ or $cos(\pi)=-1$
$=-a^2$
Calculer $\overrightarrow{BD}. \overrightarrow{AC}$.

Rappel de cours

Orthogonalité
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non nuls, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.

Aide

Les diagonales d'un carré sont perpendiculaires

Solution

On a les deux vecteurs suivants de même origine avec $\overrightarrow{AC}=\overrightarrow{BB_1}$ (en rouge)

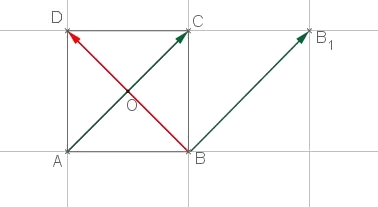
$\overrightarrow{BD}. \overrightarrow{AC}$
$=BD\times AC \times cos(\widehat{B_1BD})$
$=BD\times AC \times cos\left(\dfrac{\pi}{2}\right)$ or $cos\left(\dfrac{\pi}{2}\right)=0$
$=0$
Calculer $\overrightarrow{OB}. \overrightarrow{AB}$.

Aide

On peut utiliser le projeté orthogonal sur $(AB)$

Solution

On a les deux vecteurs suivants de même origine avec $\overrightarrow{OB}=\overrightarrow{AB_1}$ (en rouge)
Le projeté orthogonal de $B_1$ sur $(AB)$ est le point $H$ milieu de $[AB]$.