Publications MATHS-LYCEE.FR

mémo+exercices corrigés+liens vidéos

L'essentiel pour réussir la première en spécialité maths

RÉUSSIR EN MATHS, C'EST POSSIBLE!
Tous les chapitres avec pour chaque notion:
- mémo cours
- exercices corrigés d'application directe
- liens vidéos d'explications.
Il est indispensable de maîtriser parfaitement les notions de base et leur application directe pour pourvoir ensuite les utiliser dans la résolution de problèmes plus complexes.

Plus d'infos
  1. spécialité maths terminale
  2. chapitre 2 Limites de fonctions
  3. exercice corrigé nº1127

Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!

Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
PDF reservé aux abonnés
  1. On donne l'algorithme ci-dessous:

    Quel est le résultat affiché si on saisit $\varepsilon=0,1$?

    Aide

    On peut faire fonctionner cet algorithme à la main avec un tableau donnant la valeur des variables à chaque étape.

    Solution

    On a ici $\varepsilon=0,1$.

  2. En utilisant la fonction valeur absolue, quelle inégalité peut-on écrire pour remplacer la condition $-\varepsilon < \frac{x-2}{x+3}-1 < \varepsilon$?
    En déduire une écriture de la condition d'entrée dans la boucle TANT QUE avec une valeur absolue.7

    Aide

    Rappel: pour tout réel $a>0$, $ -a < x < a \Longleftrightarrow |x|< a$

    Solution

    On veut $-\varepsilon < \frac{x-2}{x+3}-1 < \varepsilon$
    soit $\vert \frac{x-2}{x+3}-1 \vert <\varepsilon$
    On peut donc remplacer la condition $ \frac{x-2}{x+3}-1 <-\varepsilon $ ou $ \frac{x-2}{x+3}-1 > \varepsilon$
  3. Saisir l'algorithme en python.
    Que s'affiche-t-il si on saisit maintenant $\varepsilon=0,01$ puis $\varepsilon=0,001$?

    Rappel de cours

    input: saisir une variable

    x=input("saisir la valeur de x") --> permet de saisir la valeur de x par l'utilisateur
    Si on veut saisir un entier par exemple: x=int(input("saisir un nombre entier"))
    Si on veut saisir un réel x=float(input("saisir un nombre"))

    Boucle TANT QUE

    while test-à-faire :   instructions de la boucle tant que

    Solution

    On dot saisir la variable (instruction input) et utiliser une boucle TANT QUE.

    Si on saisit $\varepsilon=0,01$, l'algorithme affiche $x=500$.
    Si on saisit $\varepsilon=0,001$, l'algorithme affiche $x=5000$.

    On peut utiliser aussi la fonction valeur absolue
  4. Montrer que la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x^2-6x+2$ est strictement croissante sur $[10;+\infty[$.

    Aide

    Rappel: il faut étudier le signe de la dérivée

    Solution

    $f$ est dérivable sur $[10;+\infty[$ (quotient de fonctions dérivables sur $[10;+\infty[$).
    On pose $u(x)= x-2$ et $v(x)= x+3 $
    et on a $u'(x)= 1 $ et $v'(x)= 1 $
    $f'(x)=\dfrac{u'(x)v(x)-u(x)v'(x)}{(v(x))^2}$
    $\phantom{f'(x)}=\dfrac{( 1 )( x+3 )-( x-2 )( 1 )}{( x+3 )^2}$
    $\phantom{f'(x)}=\dfrac{x+3-x+2}{( x+3 )^2}$
    $\phantom{f'(x)}=\dfrac{5}{( x+3 )^2}$
    $(x+3)^2>0$ donc $f'(x)>0$
  5. Montrer que pour tout réel $x \geq 10$, on a $f(x) <1$.

    Aide

    Comparer le numérateur et le dénominateur

    Solution

    Pour tout réel $x \geq 10$, on a:
    $x-2-(x+3)=x-2-x-3=-5$ donc $x-2 < x+3$
    $0< x-2 < x+3$ et en divisant chacun des deux membres par $x+3$ qui est strictement positif puisque $x \geq 10$, on obtient $\dfrac{x-2}{x+3} <1$
  6. En saisissant différentes valeurs de $\varepsilon$, que peut-on dire alors de $\displaystyle \lim_{x \rightarrow +\infty} \dfrac{x-2}{x+3}$?

    Rappel de cours

    limite $l$ en $+\infty$ et interprétation graphique

    La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
    $\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I

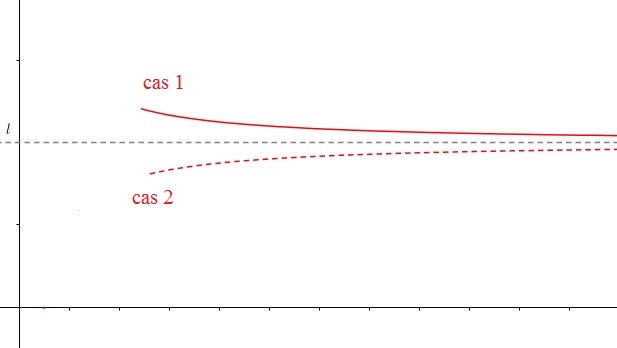
    La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$

    Aide

    On peut saisir des valeurs de plus en plus petites pour $\varepsilon$ pour avoir les conditions de la définition

    Solution

    Si on saisit $\varepsilon=10^{-4}$ on obtient $x=50000$, $\varepsilon=10^{-5}$ on obtient $x=500000$.
    donc $|f(500000)-1|< 10^{-5}$ soit $-10^{-5}< f(500000)-1 < 10^{-5}$ et $f(x) <1 $
    donc $1-10^{-5} < f(500000) < 1$
    $f$ est strictement croissante et $f(x) < 1$ donc pour tout $x > 500000 $ on a $1-10^{-5} < f(500000) < f(x) < 1 $
    On peut conjecturer que pour tout réel $\varepsilon >0$ il existe un réel $X_0$ tel que $1-\varepsilon < f(x) <1$ pour tout $x> X_0$
  7. En utilisant les limites des fonctions usuelles, retrouver le résultat précédent.

    Aide

    On peut factoriser le terme de plus haut degré.

    Solution

    Pour tout réel $x >0$, on a:
    $f(x)=\dfrac{x\left(1-\dfrac{2}{x}\right)}{x\left(1+\dfrac{3}{x}\right)}=\dfrac{1-\dfrac{2}{x}}{1+\dfrac{3}{x}}$
    $\displaystyle \lim_{x \rightarrow +\infty} 1-\dfrac{2}{x}=1$ et $\displaystyle \lim_{x \rightarrow +\infty} 1+\dfrac{3}{x}=1$

Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

exercices semblables


Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
nº1119 Limite d'un polynôme
| 5-8mn |
nº1126 Algorithme de recherche d'une limite et Python
| 8-10mn |