Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
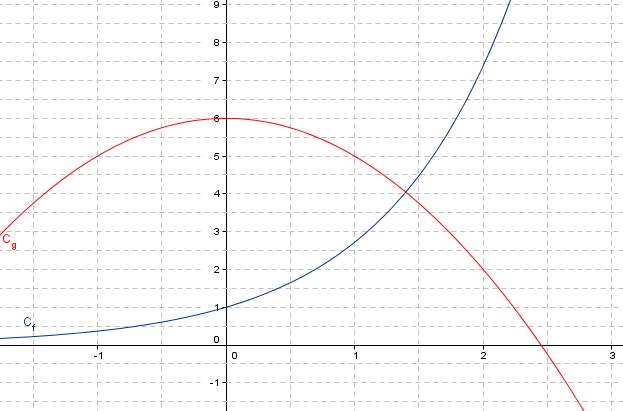
On considère les fonctions $f$ et $g$ définies sur $\mathbb{R}$ par $f(x)=6-x^2$ et $g(x)=e^x$.
On donne ci-dessous les représentations graphiques $(C_f)$ et $C_g$ respectivement des fonctions $f$ et $g$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On donne ci-dessous les représentations graphiques $(C_f)$ et $C_g$ respectivement des fonctions $f$ et $g$.

- Donner un encadrement, en unités d'aires, de l'aire $\mathcal{A}$ du domaine limité par $C_f$, $C_g$ et les droites d'équations $x=-1$ et $x=1$.
Une unité d'aire contient 4 carreaux du quadrillage.
Il faut déterminer le nombre de carreaux du quadrillage contenus dans le domaine cité et le nombre de carreaux entiers contenant le domaine cité ci-dessus.L'aire cherchée est hachurée en rouge sur la figure ci-dessous.
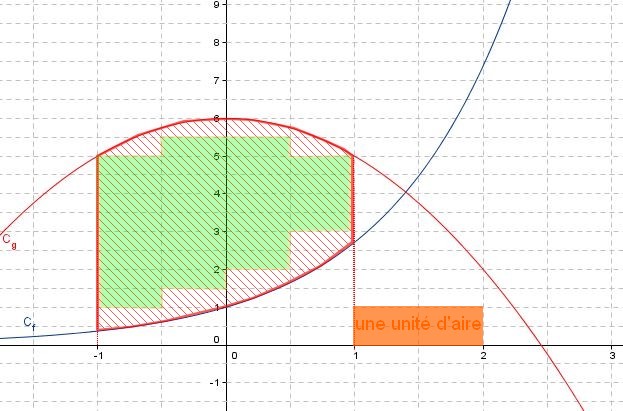
L'aire cherchée contient 30 carreaux entiers du quadrillage et une unité d'aire (en orange) contient 4 carreaux du quadrillage donc $\mathcal{A} >\dfrac{30}{4}$ soit $\mathcal{A}>7,5$ unités d'aires.
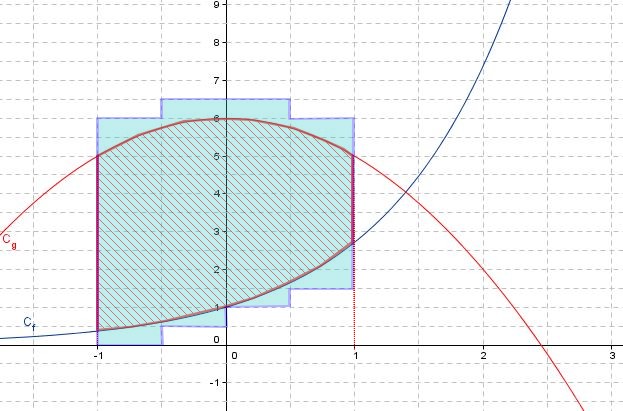
L'aire cherchée contient 44 carreaux entiers du quadrillage et une unité d'aire (en orange) contient 4 carreaux du quadrillage donc $\mathcal{A} < \dfrac{44}{4}$ soit $\mathcal{A} < 11$ unités d'aires.
- Déterminer graphiquement le signe de $f(x)-g(x)$ sur $[-1;1]$.
- Calculer la valeur exacte de cette aire.
Primitives des fonctions usuelles
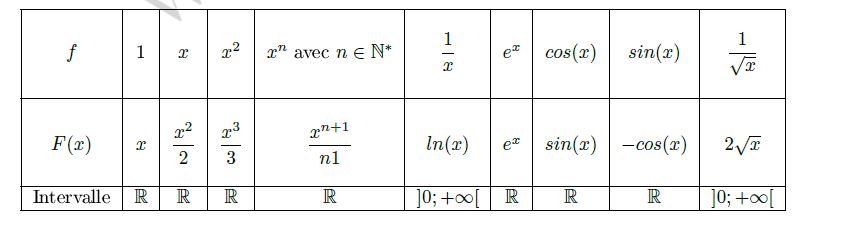
Intégrale
La fonction $f$ est continue sur $[ab]$ et $F$ est une primitive de $f$ sur $[a;b]$
$\int_a^b f(x)dx=[F(x)]_a^b=F(b)-F(a)$Il faut utiliser le fait que $f(x)>g(x)>0$ sur $[-1;1]$ et $f$ et $g$ sont continues sur $\mathbb{R}$$f$ et $g$ sont continues sur $\mathbb{R}$ donc admettent des primitives sur $\mathbb{R}$.
Sur $[-1;1]$ on a $f$ continue et $f(x)>0$ donc l'aire, en unités d'aires, $\mathcal{A}_1$ du domaine limité par $C_f$, l'axe des abscisses et les droites d'équations $x=-1$ et $x=1$ est $\int_{-1}^1 f(t)dt$.
De même sur $[-1;1]$ on a $g$ continue et $g(x)>0$ donc l'aire, en unités d'aires, $\mathcal{A}_2$ du domaine limité par $C_g$, l'axe des abscisses et les droites d'équations $x=-1$ et $x=1$ est $\int_{-1}^1 g(t)dt$.
On a $C_f$ au-dessus de $C_g$ sur $[-1;1]$ soit $f(x)\geq g(x)$
donc l'aire $\mathcal{A}$ cherchée est $\mathcal{A}_1-\mathcal{A}_2$ en unités d'aires.
$F(x)=6x-\dfrac{x^3}{3}$ est une primitive de $f$ sur $\mathbb{R}$.
$F(-1)=6\times (-1)-\dfrac{(-1)^3}{3}=-6+\dfrac{1}{3}=\dfrac{-17}{3}$
$F(1)=6\times 1-\dfrac{1^3}{3}=6-\dfrac{1}{3}=\dfrac{17}{3}$
et donc $\mathcal{A }_1=\int_{-1}^1 f(t)dt=F(1)-F(-1)=\dfrac{17}{3}-\dfrac{-17}{3}=\dfrac{34}{3}$
$G(x)=e^x$ est une primitive de $g$ sur $\mathbb{R}$.
$G(-1)=e^{-1}=\dfrac{1}{e}$
$G(1)=e^1=e$
donc on a $\mathcal{A}_2=\int_{-1}^1g(t)dt=G(1)-G(-1)=e-\dfrac{1}{e}$
$\mathcal{A}=\mathcal{A}_1-\mathcal{A}_2=\dfrac{34}{3}-e+\dfrac{1}{e}$
Penser à contrôler le calcul avec la calculatrice
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
