Publications MATHS-LYCEE.FR
Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Pour tout entier naturel $n$ on pose $I_n=\int_0^1 x^ne^{-x}dx$
- Calculer $I_0$.
Primitives des fonctions usuelles
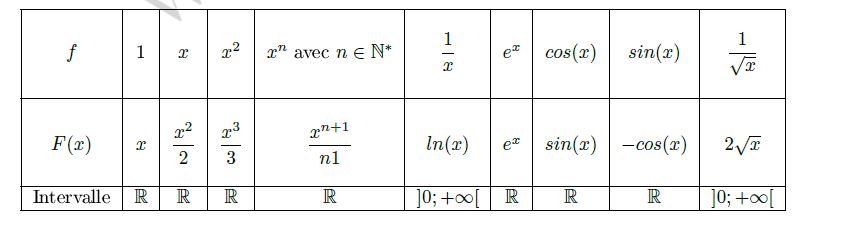Il faut chercher une primitive de $e^{-x}$ pour calculer $I_0$$\left(e^{-x}\right)'=(-x)'e^{-x}=-e^{-x}$
donc $\left(-e^{-x}\right)'=e^{-x}$
$I_0=\int_0^1 x^0e^{-x}dx=\int_0^1 e^{-x} dx =[-e^{-x}]_0^1=-e^{-1}-(-e^{-0})=-e^{-1}+1$
- Montrer que la suite $(I_n)$ est décroissante.
Étude des variations(différence de deux termes consécutifs)
Pour étudier les variations de $(u_n)$, il faut comparer $u_{n+1}$ et $u_n$.
Exprimer $u_{n+1}-u_n$ en fonction de $n$
Étudier le signe de l'expression obtenue
Si $u_{n+1}-u_n >0 $ alors$u_{n+1} >u_n$ et donc la suite $(u_n)$ est croissante.
Si $u_{n+1}-u_n <0 $ alors$u_{n+1} < u_n$ et donc la suite $(u_n)$ est décroissante.Intégrale d'une fonction continue positive
Soit $f$ continue sur $[a;b]$ (avec $a < b$) et $f(x)\geq 0$ sur $[a;b]$
alors $\displaystyle \int_a^b f(x)dx \geq 0$On peut étudier le signe de $I_{n+1}-I_n$
Si $f$ est positive sur $[a;b]$ avec $a < b$ alors $\int_a^b f(x()dx>0$$I_{n+1}-I_n=\int_0^1 x^{n+1}e^{-x}dx-\int_0^1 x^ne^{-x} dx$
$\phantom{I_{n+1}-I_n}=\int_0^1 x^{n+1}e^{-x}- x^ne^{-x} dx$
$\phantom{I_{n+1}-I_n}=\int_0^1 x^{n}\times xe^{-x}- x^ne^{-x} dx$
$\phantom{I_{n+1}-I_n}=\int_0^1 x^{n}e^{-x}(x-1) dx$
Si on pose $f(x)=x^n(x-1)e^{-x}$ sur $[0;1]$
on a alors $x^n\geq 0$, $x-1\leq 0$ et $e^{-x}>0$ donc $f(x)\leq 0$
et donc $\int_0^1 f(x)dx\leq 0$
On a donc $I_{n+1}-I_n\leq 0$
- Montrer que la suite $(I_n)$ est minorée et en déduire que $(I_n)$ est convergente.
Limite d'une suite majorée ou minorée
Si la suite $(u_n)$ est croissante et majorée alors elle est convergente.
Si la suite $(u_n)$ est décroissante et minorée alors elle est convergenteOn a $x^ne^{-x} \geq 0$ sur $[0;1]$Pour tout réel $x\in[0;1]$ on a $e^{-x}>0$ et $x^n \geq 0$.
donc $x^ne^x\geq 0$ et on a alors $\int_0^1 x^n e^{-x} dx\geq 0$
donc $I_n \geq 0$
$(I_n)$ est décroissante et minorée
- Montrer que pour tout entier naturel $n$ on a $x^ne^{-x} < x^n$ avec $x\in[0;1]$ et en déduire la limite de la suite $(I_n)$.
pour $x\in [0;1]$, on a $e^x > 1$ et $e^{-x}=\dfrac{1}{e^x}$ donc $0La fonction exponentielle est continue et strictement croissante avec $e^0=1$
donc pour tout réel $x\in [0;1]$, on a $ 0 < e^{x}\geq 1$
donc $\dfrac{1}{ e^{x}} \leq 1$ soit $0< e^{-x} \leq 1$
donc $x^ne^{-x} \leq x^n$
donc $\int_0^1 x^ne^{-x}dx \leq \int_0^1 x^ndx$
$\int_0^1 x^n dx =\left[\dfrac{x^{n+1}}{n+1}\right]_0^1=\dfrac{1}{n+1}-\dfrac{0}{n+1}=\dfrac{1}{n+1}$
donc $0 \leq I_n \leq \dfrac{1}{n+1}$
$\displaystyle \lim_{n \rightarrow +\infty}\dfrac{1}{n+1}=0$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.