Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Le plan est muni d'un repère orthonormé $(O;\overrightarrow{i};\overrightarrow{j})$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- On note $a=3-3i$ et $b=-a$.
- Ecrire $b$ sous forme exponentielle.
Forme trigonométrique
Soit $z=x+iY$ un complexe.
Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
Cette forme est appelée forme trigonométrique} de $z$.Forme exponentielle
$z$ est un complexe d'argument $\alpha$
La forme exponentielle de $z$ est $z=|z|e^{i\alpha}$Il faut calculer $|b|$ et on a $cos(arg(b))=\dfrac{-3}{|b|}$ et $sin(arg(b))=\dfrac{3}{|b|}$$b=-a=-3+3i$
$|b|=\sqrt{(-3)^2+3^2}=\sqrt{18}=3\sqrt{2}$
$b=3\sqrt{2}\left(\dfrac{-3}{3\sqrt{2}}+i\dfrac{3}{3\sqrt{2}}\right)=3\sqrt{2}\left(\dfrac{-1}{\sqrt{2}}+i\dfrac{1}{\sqrt{2}}\right)$
Si on note $\theta=arg(b)$, on a alors:
$\begin{cases} cos(\theta)=\dfrac{-1}{\sqrt{2}}\\ sin(\theta)=\dfrac{1}{\sqrt{2}} \end{cases} \Longleftrightarrow \begin{cases} cos(\theta)=-\dfrac{\sqrt{2}}{\sqrt{2}\sqrt{2}}\\ sin(\theta)=\dfrac{\sqrt{2}}{\sqrt{2}\sqrt{2}} \end{cases} \Longleftrightarrow \begin{cases} cos(\theta)=-\dfrac{\sqrt{2}}{2}\\ sin(\theta)=\dfrac{\sqrt{2}}{2} \end{cases} $
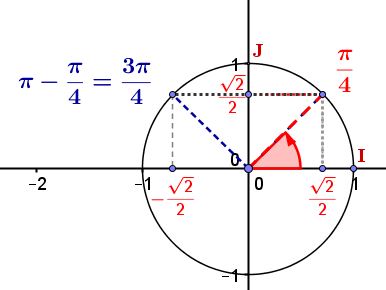
donc $\theta=\dfrac{3\pi}{4}$ ($2\pi$).
- Déterminer l'affixe $c$ du point $C$ tel que $OB=OC$ et $(\overrightarrow{OB};\overrightarrow{OC})=\dfrac{\pi}{2}$ ($2\pi$).
$OB=|b|$ et $(\overrightarrow{OB};\overrightarrow{OC})=arg\left(\dfrac{c}{b}\right)=arg(c)-arg(b)$$OB=|b|=|-3+3i|=\sqrt{(-3)^2+3^2}=\sqrt{18}=3\sqrt{2}$
$OC=OB \Longleftrightarrow |c|=|b| \Longleftrightarrow |c|=3\sqrt{2}$
$(\overrightarrow{OB};\overrightarrow{OC})=arg(c)-arg(b)$ ($2\pi$)
donc $arg(c)-arg(b)=\dfrac{\pi}{2}$ ($2\pi$) soit $arg(c)=\dfrac{\pi}{2}+\dfrac{3\pi}{4}=\dfrac{5\pi}{4}$ ($2\pi$)
La forme algébrique de $c$ est donc:
$c=3\sqrt{2}\left(cos\left(\dfrac{5\pi}{4}\right)+isin\left(\dfrac{5\pi}{4}\right)\right)$
$\phantom{c}=3\sqrt{2}\left(\dfrac{-\sqrt{2}}{2}+i\dfrac{-\sqrt{2}}{2}\right)$
$\phantom{c}=-3-3i$
Penser à contrôler le résultat avec la calculatrice
La mesure principale de $arg(c)$ est $\dfrac{5\pi}{4}-2\pi=\dfrac{-3\pi}{4}$ - Déterminer l'affixe $d$ du point $D$ tel que $ABCD$ soit un parallélogramme.
Les affixes des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$ doivent être égales.$ABCD$ est un parallélogramme
$\Longleftrightarrow \overrightarrow{AB}=\overrightarrow{DC}$
$\Longleftrightarrow b-a=c-d$
$\Longleftrightarrow -3+3i-(3-3i)=-3-3i-d$
$\Longleftrightarrow -3+3i-3+3i=-3-3i-d$
$\Longleftrightarrow -3+9i=-d$
$\Longleftrightarrow d=3-9i$
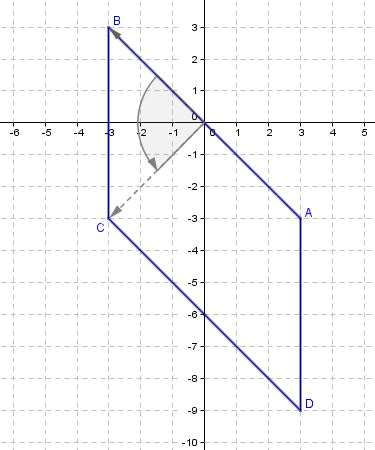
- Ecrire $b$ sous forme exponentielle.
- On veut déterminer l'ensemble $\mathcal{E}$ des points $M$ tels que $||\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}||=2BD$.
- Montrer que $D$ appartient à $\mathcal{E}$.
ABCD parallélogramme donc $\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}$$ABCD$ parallélogramme donc $\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}$
donc $||\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}||=||\overrightarrow{DB}+\overrightarrow{DB}||=||2\overrightarrow{DB}||=2DB$
- On note $z$ l'affixe de $M$.
Montrer que $M\in \mathcal{E} \Longleftrightarrow |z+1+i|=4\sqrt{5}$
En déduire la nature de $\mathcal{E}$.L'affixe du vecteur $\overrightarrow{MA}$ est $z-a$
Il faut donc calculer le module de $z-a+z-b+z-c$L'affixe du vecteur $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$ est :
$a-z+b-z+c-z=3-3i-3+3i-3-3i-3z=-3-3i-3z$
et $BD=|d-b|=|3-9i-(-3+3i)|=|6-12i|=\sqrt{6^2+(-12)^2}=\sqrt{180}=6\sqrt{5}$
$M\in \mathcal{E} \Longleftrightarrow ||\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}||=2BD$
$\phantom{M\in \mathcal{E}} \Longleftrightarrow|-3-3i-3z|=2\times |d-b|$
$\phantom{M\in \mathcal{E}} \Longleftrightarrow |-3(1+i+z)|=2\times 6\sqrt{5}$
$\phantom{M\in \mathcal{E}} \Longleftrightarrow 3|1+i+z|=12\sqrt{5}$
$\phantom{M\in \mathcal{E}} \Longleftrightarrow |z+1+i|=4\sqrt{5}$
Si on pose $I$ d'affixe $z_I=-1-i$, on a alors
$|z+1+i|=|z-(-1-i)|=|z-z_I|=IM=4\sqrt{2}$
donc $M$ appartient au cercle de centre $I(-1;-1)$ et rayon $4\sqrt{2}$.
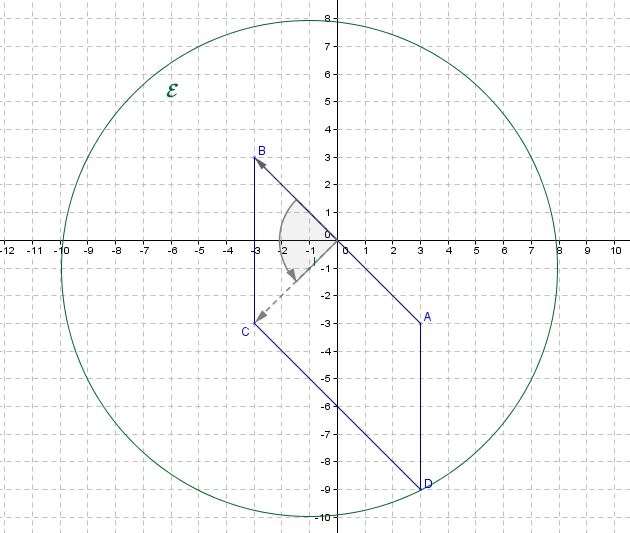
- Montrer que $D$ appartient à $\mathcal{E}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
