Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Une société vend des forfaits pour téléphones portables et deux formules sont proposées:
- Formule A: un forfait de 15 euros par mois et 11 centimes d'euro par minute d'appel
- Formule B: un forfait de 20 euros par mois et 1 centime d'euro par minute d'appel
On note $x$ le nombre de minutes de communication dans le mois, $f(x)$ le coût total des communications (forfait+appels) par mois avec la formule A et $g(x)$ le coût total avec la formule B.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- Formule A: un forfait de 15 euros par mois et 11 centimes d'euro par minute d'appel
- Formule B: un forfait de 20 euros par mois et 1 centime d'euro par minute d'appel
On note $x$ le nombre de minutes de communication dans le mois, $f(x)$ le coût total des communications (forfait+appels) par mois avec la formule A et $g(x)$ le coût total avec la formule B.
- Exprimer $f(x)$ et $g(x)$ en fonction de $x$.
On paye $x\times 0,11$ euros pour les communications avec la formule A plus le forfaitAvec la formule A, pour $x$mn, on va payer pour les communications $0,11x$ euros et il faut ajouter le forfait de 15 euros
De même, avec la formule B, pour $x$mn, on va payer pour les communications $0,01x$ euros et il faut ajouter le forfait de 20 euros
- Quelle est la nature des fonctions $f$ et $g$?
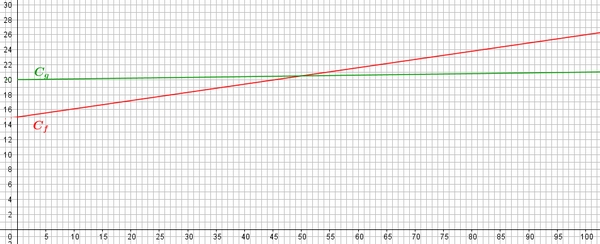
Représenter ces deux fonctions dans le repère ci-dessous.
- Résoudre l'équation $f(x)=g(x)$ et contrôler sur le graphique.
$f(x)=g(x) \Longleftrightarrow 0,11x+15=0,01x+20$
$\phantom{f(x)=g(x)} \Longleftrightarrow 0,11x-0,01x=20-15$
$\phantom{f(x)=g(x)} \Longleftrightarrow 0,10x=5$
$\phantom{f(x)=g(x)} \Longleftrightarrow x=\dfrac{5}{0,1}$
$\phantom{f(x)=g(x)} \Longleftrightarrow x=50$
Graphiquement,la solution de l'équation $f(x)=g(x)$ est l'abscisse du point d'intersection des deux courbes. - En déduire quelle formule est la plus avantageuse en fonction du nombre $x$ de minutes d'appels.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.