Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Résoudre les inéquations suivantes en utilisant la représentation graphique de la fonction carré donnée ci-dessous.
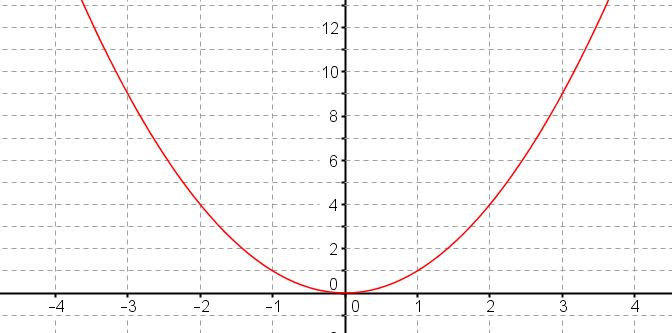
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

- $x^2-2<5$
Il faut se ramener à une inéquation de la forme $x^2 < k$
On peut ensuite utiliser la représentation graphique de la fonction carré$x^2-2 <5 \Longleftrightarrow x^2< 7$
$x^2=7 \Longleftrightarrow x=\sqrt{7}$ ou $x=-\sqrt{7}$.
Graphiquement, les solutions de l'inéquation $x^2 < 7$ sont les abscisses (en vert) des points de la courbe (en bleu) situés strictement en-dessous de la droite d'équation $y=7$(en gris)
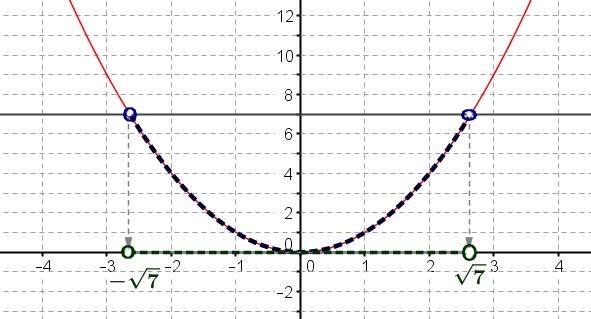
- $x^2+8 \leq 4$
Il faut se ramener à une inéquation de la forme $x^2 \leq k$
le minimum de la fonction carré est 0.$x^2+8 \leq 4 \Longleftrightarrow x^2 \leq -4$.
Sur $\mathbb{R}$, le minimum de la fonction carré est 0 donc $x^2 \geq 0$ pour tout réel $x$.
$x^2$ ne peut donc pas être inférieur ou égal à $-4$
- $(x-1)^2<9$
En utilisant éventuellement la courbe, il faut déterminer d'abord les valeurs pour lesquelles $x-1$ est tel que $(x-1)^2 <9$Graphiquement, les solutions le carré est inférieur à 7 sont les abscisses (en vert) des points de la courbe (en bleu) situés strictement en-dessous de la droite d'équation $y=9$(en gris)
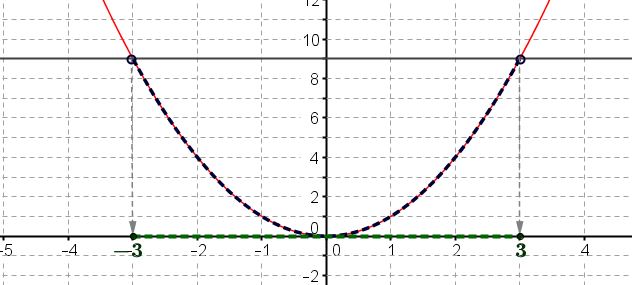
Il faut donc $-3< x-1 < 3$.
$-3< x-1 < 3 \Longleftrightarrow -3+1< x < 3+1 \Longleftrightarrow -2< x <4$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
