Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
$f$ est la fonction inverse définie sur $\mathbb{R}^*$.
Déterminer dans chaque cas le maximum et le minimum de $f$ sur l'intervalle $I$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Déterminer dans chaque cas le maximum et le minimum de $f$ sur l'intervalle $I$.
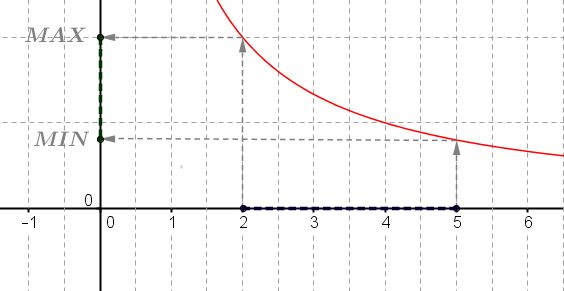
- $I=[2;5]$
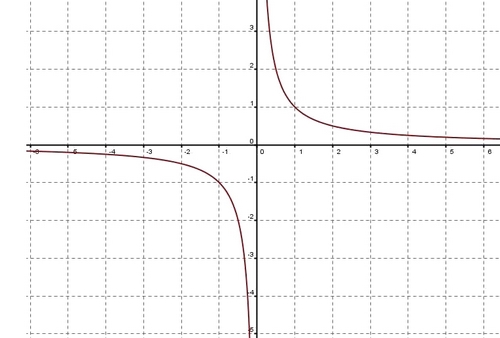
Fonction inverse
La fonction inverse est définie sur $\mathbb{R}^*$ (tous les réels sauf $0$)
et est strictement décroissante sur $]-\infty;[$ et sur $]0;+\infty[$.
La représentation graphique de la fonction inverse est une hyperbole.
 Il faut utiliser les variations de la fonction inverse sur $]0;+\infty[$La fonction inverse est strictement décroissante sur $]0;+\infty[$
Il faut utiliser les variations de la fonction inverse sur $]0;+\infty[$La fonction inverse est strictement décroissante sur $]0;+\infty[$
donc le maximum de $f$ est $f(2)=\dfrac{1}{2}$ et le minimum de $f$ est $f(5)=\dfrac{1}{5}$.
Graphiquement, on a:
L'ordre des images est inversé. - $I=[-4;-1]$
- $I=\left[\dfrac{1}{4};\dfrac{1}{2}\right]$
Il faut utiliser les variations de la fonction inverse sur $]0;+\infty[$La fonction inverse est strictement décroissante sur $]0;+\infty[$
donc le maximum de $f$ est $f\left(\dfrac{1}{4}\right)=\dfrac{1}{\frac{1}{4}}=4$
et le minimum de $f$ est $f\left(\dfrac{1}{2}\right)=\dfrac{1}{\frac{1}{2}}=2$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
