Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On considère les fonction $f$, $g$ définies par $f(x)=x^2$ et $g(x)=\dfrac{-1}{2}x+3$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
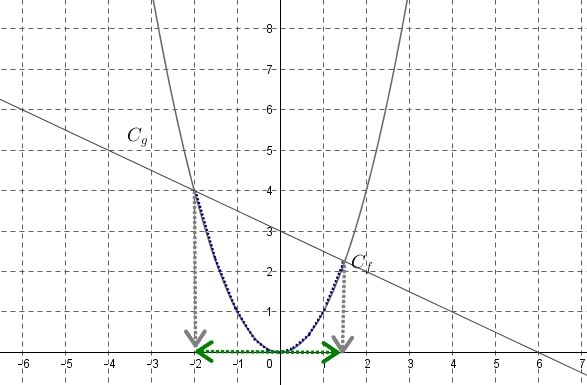
- Dans un repère orthonormé, tracer $C_f$ et $C_g$ les représentations graphiques respectivement des fonctions $f$ et $g$.
Fonction affine
Une fonction afffine est définie sur $\mathbb{R}$ par $f(x)=ax+b$.
La représentation graphique d'une fonction affine est une droite coupant l'axe des ordonnées au point $(0;b)$ et l'axe des abscisses au point $\left(\dfrac{-b}{a}\right)$ (si $a\neq 0$).
Si $a=0$ alors la droite est parallèle à l'axe des abscisses.On peut utiliser le MENU TABLE de la calculatrice pour placer suffisament de points afin d'avoir un tracé précisLa représentation graphique de la fonction carré est une parabole de sommet $O(0;0)$.
$g$ est une fonction affine donc sa représentation graphique est une droite de coefficient directeur $a=\dfrac{-1}{2}$ et ordonnée à l'origine $b=3$.
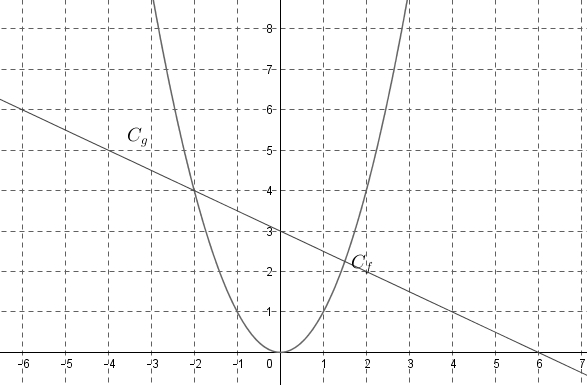
- Résoudre graphiquement l'inéquation $x^2 < \dfrac{-1}{2}x+3$.
- Montrer que résoudre l'inéquation $f(x) < g(x)$ revient à étudier le signe de $\left(x-\dfrac{3}{2}\right)(x+2)$.
On peut calculer $f(x)-g(x)$ et développer $\left(x-\dfrac{3}{2}\right)(x+2)$$f(x)< g(x) \Longleftrightarrow x^2< \dfrac{-1}{2}x+3 \Longleftrightarrow x^2+ \dfrac{1}{2}x-3 < 0$
$\left(x-\dfrac{3}{2}\right)(x+2)=x^2+2x-\dfrac{3}{2}x-\dfrac{3}{2}\times 2=x^2+\dfrac{1}{2}x-3$
Pour comparer deux nombres, on peut étudier le signe de leur différence donc pour résoudre l'inéquation $f(x)< g(x)$ on peut étudier le signe de $f(x)-g(x)=\left(x-\dfrac{3}{2}\right)(x+2)$
- En déduire l'ensemble de solution de l'inéquation $x^2 < \dfrac{-1}{2}x+3$ et comparer avec le résultat obtenu graphiquement.
Il faut étudier le signe du produit de deux facteurs donc dresser un tableau de signes.$x-\dfrac{3}{2}=0 \Longleftrightarrow x=\dfrac{3}{2}$
$x+2=0 \Longleftrightarrow x=-2$
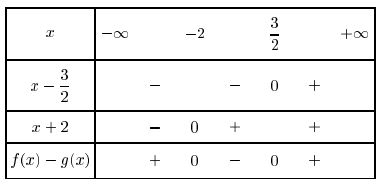
donc $f(x)-g(x) <0$ pour $x\in \left]-2;\dfrac{3}{2}\right[$
On retrouve bien le résultat graphique avec $-2 < x <1,5$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.