Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On considère les fonctions $f$ et $g$ définies par $f(x)=\dfrac{1}{x}$ et $g(x)=3x+2$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- Quel est l'ensemble de définition $D_f$ de $f$? $D_g$ de $g$?
Ensemble de définition
L'ensemble de définition d'une fonction $f$ est l'ensemble des valeurs pour lesquelles on peut calculer l'image par $f$.
Par exemple, l'ensemble de définition de la fonction $f$ définie par $f(x)=\dfrac{1}{x+2}$ est $\mathbb{R}\setminus \lbrace -2\rbrace$ car le dénominateur doit être différent de $0$.Il faut que le dénominateur soit différent de 0 donc $D_f=\mathbb{R} \setminus \lbrace 0 \rbrace=\mathbb{R}^{*}$
$g$ est une fonction affine donc $D_g=\mathbb{R}$.
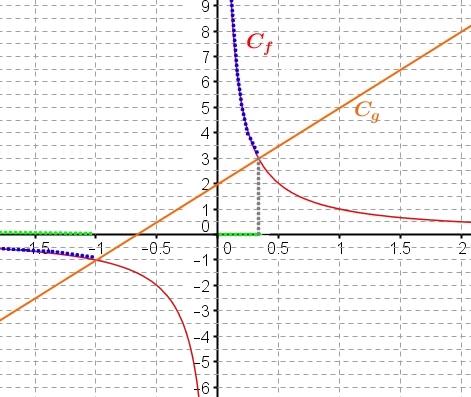
- Avec la calculatrice ou bien geogebra, représenter dans un même repère les courbes représentatives $C_f$ et $C_g$ des fonctions $f$ et $g$ puis conjecturer à laide du graphique les valeurs de $x$ pour lesquelles $f(x)>g(x)$.
- Montrer que pour tout réel $x$, $(x+1)(-3x+1)=-3x^2-2x+1$
puis résoudre l'inéquation $f(x) > g(x)$ par le calcul.Il faut se ramener à l'étude du signe d'un quotient (tableau de signes).Pour tout réel $x$, on a:
$(x+1)(-3x+1)=-3x^2+x-3x+1=-3x^2-2x+1$
$-3x^2-2x+1$ $f(x) > g(x) \Longleftrightarrow \dfrac{1}{x} > 3x+2$
$\phantom{f(x) > g(x)} \Longleftrightarrow \dfrac{1}{x} - 3x-2 > 0$
$\phantom{f(x) > g(x)} \Longleftrightarrow \dfrac{1-3x^2-2x}{x} > 0$
$\phantom{f(x) > g(x)} \Longleftrightarrow \dfrac{(x+1)(-3x+1)}{x} > 0$ car $-3x^2-2x+1=(x+1)(-3x+1)$
$x+1$ s'annule pour $x=-1$
$-3x+1$ s'annule pour $x=\dfrac{1}{3}$
$x$ s'annule pour $x=0$

donc $f(x) > g(x)$ (zone bleue) pour $x\in ]-\infty;-1[\cup \left]0;\dfrac{1}{3}\right[$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.