Une urne A contient deux boules avec les numéros 1 et 2.
Une urne B contient trois boules avec les numéros 1, 2 et 3.
Une urne C contient deux boules avec les numéros 1 et 2.
On prend une boule dans l'urne A et on note $x$ le numéro obtenu, une boule dans l'urne B et on note $y$ le numéro obtenu puis une boule dans l'urne C et on note $z$ le numéro obtenu.
On a donc un triplet $(x;y;z)$ avec les trois chiffres obtenus.

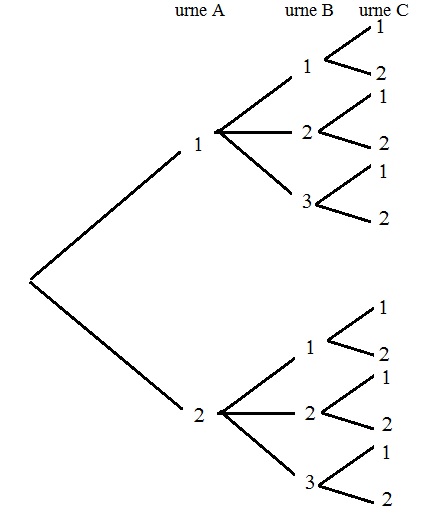
1. A l'aide d'un arbre, déterminer le nombre de triplets $(x;y;z)$ possibles.

   Aide

   On a donc deux branches au départ pour le tirage dans l'urne A puis trois branches pour le tirage dans l'urne B puis deux branches pour le tirage dans l'urne C

   Solution

   On a donc l'arbre suivant:
   
   Il y a donc $2\times 3\times 2=12$ cas possibles.
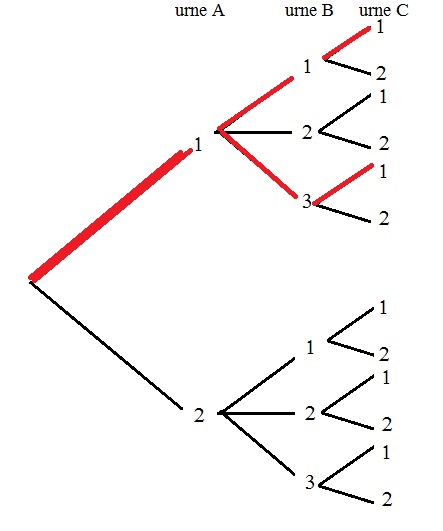
2. Quelle est alors la probabilité d'obtenir le triplet $(1;2;1)$?

   Rappel de cours

   Probabilité avec une loi équirépartie

   ---

   Dans le cas d'une loi équirépartie, la probabilité d'un événement A est $p(A)=\dfrac{\text{nombre de cas favorables}}{\text{nombre de cas possibles}}$

   Solution

   Il y a un cas parcours possible sur l'arbre permettant d'obtenir $(1;2;1)$
   donc la probabilité d'obtenir $(1;2;1)$ est $\dfrac{1}{12}$.
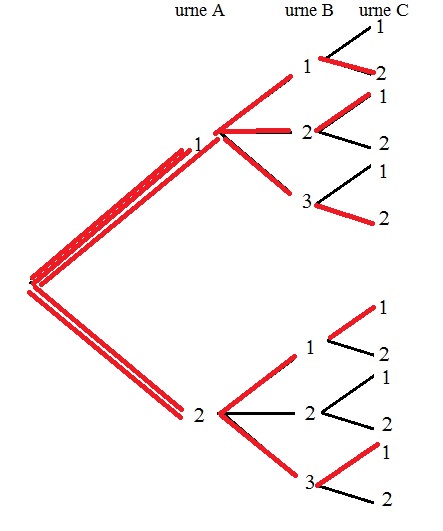
3. Quelle est la probabilité d'obtenir exactement une fois le chiffre 2 dans le triplet $(x;y;z)$?

   Aide

   Il faut déterminer tous les parcours sur l'arbre contenant exactement une fois le chiffre 2

   Solution

   On repère en rouge les parcours contenant une fois le chiffre 2.
   
   Il y a 5 parcours sur l'arbre contenant une fois le chiffre 2
   donc la probabilité d'obtenir une seule fois le chiffre 2 dans $(x;y;z)$ est $\dfrac{5}{12}$.
4. Quelle est la probabilité de l'événement $E$: "obtenir un triplet $(x;y;z)$ sans le chiffre 2"?

   Aide

   Il faut déterminer tous les parcours sur l'arbre ne contenant pas le chiffre 2

   Solution

   On repère en rouge les parcours contenant ne contenant pas le chiffre 2.
   
   Il y a 2 parcours sur l'arbre ne contenant pas le chiffre 2
   on a $p(E)=\dfrac{2}{12}=\dfrac{1}{6}$
   donc la probabilité d'obtenir un triplet sans le chiffre 2 est $\dfrac{1}{6}$.
5. En déduire la probabilité d'obtenir au moins une fois le chiffre 2 dans le triplet $(x;y;z)$.

   Rappel de cours

   Notations des événements et probabilités

   ---

   $\Omega$ est l'événement certain et $p(\Omega)=1$
   $\oslash$ est l'événement impossible et $p(\oslash)=0$
   $\overline{A}$ est l'événement contraire de A et est composé de toutes les issues de $\Omega$ qui ne sont pas contenue dans A et $p(\overline{A})=1-p(A)$

   Aide

   "Au moins une fois le chiffre 2" est le contraire de "aucun chiffre 2"

   Solution

   Si on note $F$ l'événement " le triplet $(x;y;z)$ ne contient au moins une fois le chiffre 2"
   alors $F$ est le contraire de l'événement $E$
   et $p(F)=1-p(E)=1-\dfrac{1}{6}=\dfrac{5}{6}$
   La probabilité d'obtenir au moins une fois le chiffre 2 est $\dfrac{5}{6}$.