Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Résoudre les inéquations suivantes
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- $x^2-4x+3>0$
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
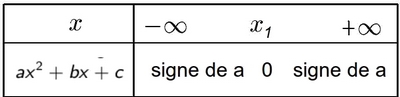
- Cas $\Delta<0$ (aucune racine)
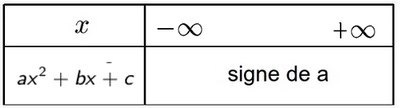 Rechercher les racines de $x^2-4x+3$
Rechercher les racines de $x^2-4x+3$
Dresser le tableau de signe de $x^2-4x+3$
Donner l'ensemble de solution de l'inéquationIci on a $a=1$, $b=-4$ et $c=3$
$\Delta=b^2-4ac=(-4)^2-4\times 1\times 3=16-12=4$
$\Delta>0$ donc il y a deux racines:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{4-2}{2}=1$
$x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{4+2}{2}=3$
Etude du signe de $x^2-4x+3$

$x^2-4x+3>0$ pour $x\in ]-\infty;1[\cup ]3;+\infty[$
On pouvait éviter de calculer $\Delta$.
La somme des coefficients est nulle, $a+b+c=0$
donc $x_1=1$ est une racine de $x^2-4x+3$
On peut utiliser le produit des racines soit $x_1\times x_2=\dfrac{c}{a}$
donc $x_2=\dfrac{3}{1}=3$ - $-2x^2+5x-2>0$
Rechercher les racines de $-2x^2+5x-2$
Dresser le tableau de signe de $-2x^2+5x-2$
Donner l'ensemble de solution de l'inéquationIci on a $a=-2$, $b=5$ et $c=-2$
$\Delta=b^2-4ac=5^2-4\times (-2)\times (-2)=25-16=9$
$\Delta>0$ donc il y a deux racines:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-5-3}{-4}=\dfrac{-8}{-4}=2$
et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-5+3}{-4}=\dfrac{-2}{-4}=\dfrac{1}{2}$
Etude du signe de $-2x^2+5x-2$

$x^2-4x+3>0$ pour $x\in \left]\dfrac{1}{2};2\right[ $
- $-2x^2+5x-4>0$
$\Delta=b^2-4ac=5^2-4\times (-2)\times (-4)=25-32=-7$
$\Delta <0$ donc il n'y a aucune racine
et $-2x^2+5x-4$ est du signe de $a=-2$ coefficient de $x^2$ soit:

donc $-2x^2+5x-4$ est toujours strictement négatif et cette inéquation n'admet aucune solution.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Fiche méthode
Si cet exercice vous pose problème, nous vous conseillons de consulter la fiche méthhode.
Inéquations commentées pas à pas
Exemples de résolution d'inéquations en utilisant le signe du polynôme du second degré
infos: | 8-12mn |
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
