Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On considère la fonction $f$ définie sur $\mathbb{R}^*$ par $f(x)=\dfrac{2}{x}$ et on note $C_f$ sa courbe représentative (une hyperbole) dans un repère orthonormé.
La droite $(D)$ a pour équation réduite $y=\dfrac{1}{2}x-\dfrac{3}{2}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
La droite $(D)$ a pour équation réduite $y=\dfrac{1}{2}x-\dfrac{3}{2}$.
- On donne $C_f$ dans le repère ci-dessous.
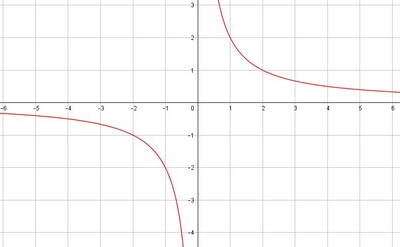
Tracer $D$ dans ce repère et déterminer graphiquement les solutions de l'équation $\dfrac{2}{x}=\dfrac{1}{2}x-\dfrac{3}{2}$.Il faut déterminer les coordonnées de deux points de $D$ en choisissant par exemple $x=0$ puis $x=2$ et en calculant $y$
Les solutions de l'équation sont les abscisses des points d'intersection de $C_f$ et de $D$si $x=0$ alors $y=\dfrac{1}{2}\times 0-\dfrac{3}{2}=\dfrac{-3}{2}$.
si $x=2$ alors $y=\dfrac{1}{2}\times 2-\dfrac{3}{2}=\dfrac{-1}{2}$.
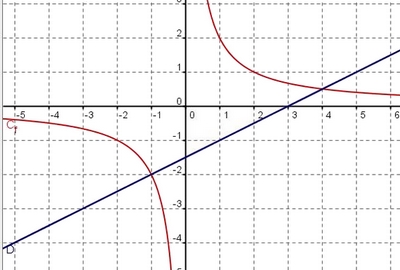
Les solutions de l'équation $f(x)=\dfrac{1}{2}x-\dfrac{3}{2}$ sont les abscisses des points d'intersection de $C_f$ et de $D$
- Résoudre l'équation $\dfrac{2}{x}=\dfrac{1}{2}x-\dfrac{3}{2}$ et retrouver le résultat obtenu graphiquement.
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.On peut multiplier les deux membres par $2$ puis utiliser les produits en croix égaux pour se ramener à une équation de la forme $ax^2+bx+c=0$$\dfrac{2}{x}=\dfrac{1}{2}x-\dfrac{3}{2}$
$\Longleftrightarrow \dfrac{4}{x}=x-3$ (on multiplie les deux membres par $2$)
$\Longleftrightarrow 4=(x-3)\times x$ (produits en croix égaux)
$\Longleftrightarrow 4=x^2-3x$
$\Longleftrightarrow x^2-3x-4=0$
$\Delta=b^2-4ac=(-3)^2-4\times 1\times (-4)=25$
$\Delta>0$ donc il y a deux solutions
$x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{ 3 +5 }{2 }=4$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3 -5 }{ 2 }=-1$
Le résultat obtenu est cohérent avec les lectures graphiques
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
nº655 Intersection droite et parabole
| 5-8mn |
nº625 Intersection parabole -droite
| 15-20mn |
nº1026 Position relative d'une droite et d'une hyperbole
| 10-15mn |
| 5-8mn |
nº625 Intersection parabole -droite
| 15-20mn |
nº1026 Position relative d'une droite et d'une hyperbole
| 10-15mn |
