Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Une entreprise fabrique des appareils électroniques de haute technologie.
Le coût total de fabrication de $q$ appareils est $C(q)=50q-q^2+20$.
Le coût est exprimé milliers d'euros avec $q\in[0;50]$.
On admet que chaque appareil fabriqué est vendu au prix unitaire de 10500 euros et que toute la production est vendue.
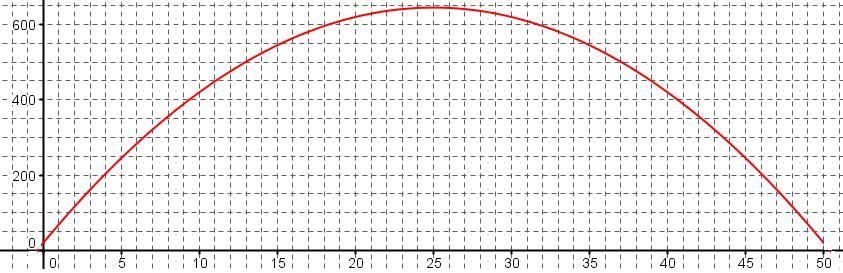
La figure ci-dessous, donne la courbe représentative de la fonction coût total dans un repère orthogonal.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Le coût total de fabrication de $q$ appareils est $C(q)=50q-q^2+20$.
Le coût est exprimé milliers d'euros avec $q\in[0;50]$.
On admet que chaque appareil fabriqué est vendu au prix unitaire de 10500 euros et que toute la production est vendue.
La figure ci-dessous, donne la courbe représentative de la fonction coût total dans un repère orthogonal.

- Déterminer la quantité d'appareils à produire pour que le coût de production soit maximal.
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: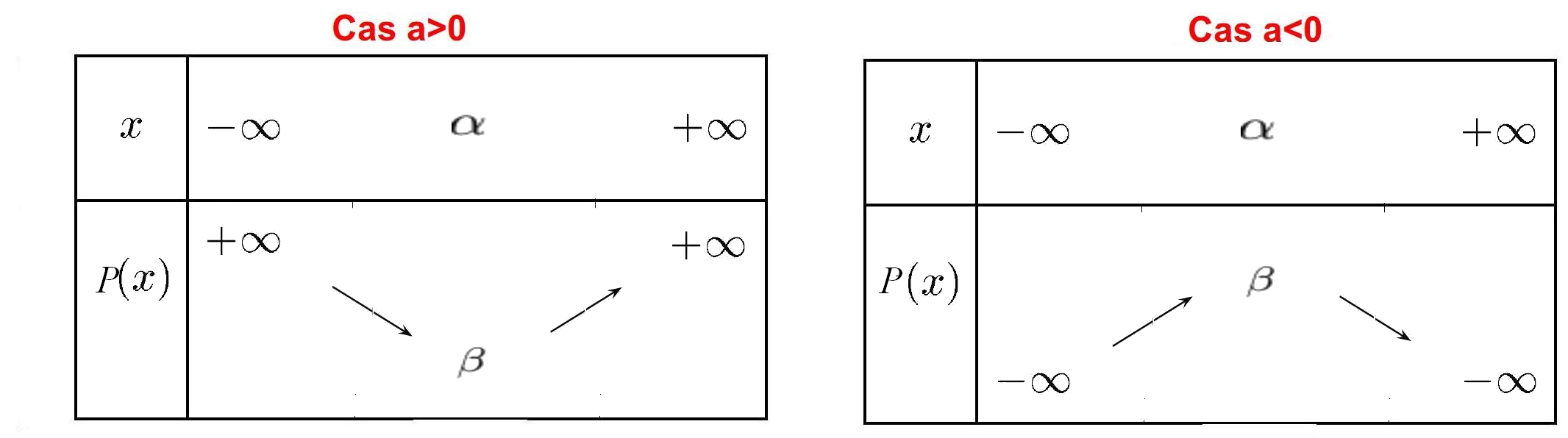
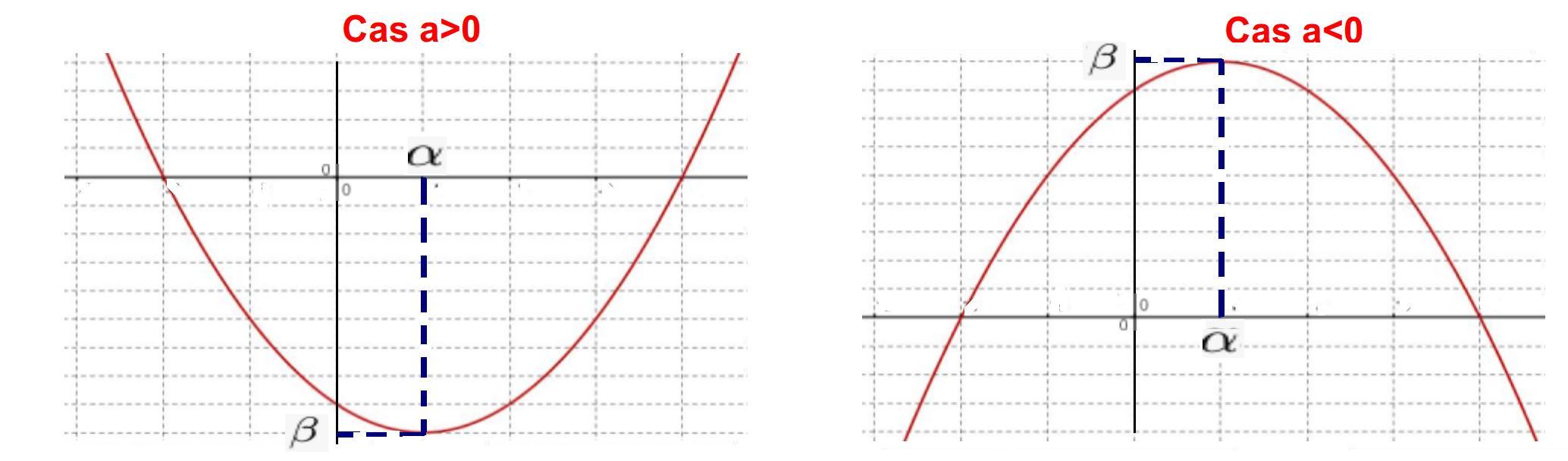 Il faut déterminer les coordonnées du sommet de la parabole et dresser le tableau de variation de la fonction $C$.
Il faut déterminer les coordonnées du sommet de la parabole et dresser le tableau de variation de la fonction $C$.
L'expression de $C$ n'est pas ordonnée selon les puissances décroissante de $q$.Pour éviter les erreurs, on écrit $C(q)$ en ordonnant selon les puissances décroissantes de la quantité $q$:
$C(q)=50q-q^2+20=-q^2+50q+20$
$\alpha=\dfrac{-b}{2a}=\dfrac{-50}{-2}=25$
$\beta=C(\alpha)=C(25)=-25^2+50\times 25+20=645$
Le coefficient de $x^2$ est $a=-1$ donc on a:
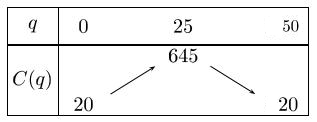
la variable est $q$ (ne pas écrire $C(x)$ par exemple) et les coûts sont donnés en milliers d'euros. - Exprimer la recette $R(q)$, en milliers d'euros, en fonction de $q$.
Si on vend $q$ objets au prix unitaire de $p$ euros, la recette engendrée est de $p\times q$ euros.
es prix sont à utiliser en milliers d'eurosChaque appareil est vendu au prix unitaire de $10500$ euros soit $10,5$ milliers d'euros.
La recette pour $q$ appareils vendus est alors de $R(q)=10,5\times q$ milliers d'euros.
- Exprimer alors le bénéfice $B(q)$, en milliers d'euros, réalisé par cette entreprise en fonction de $q$.
- Déterminer alors la quantité à produire pour que l'entreprise ne soit pas en déficit
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Il faut déterminer les valeurs de $q$ pouir lesquelles on a un bénéfice positif soit $B(q)>0$$B(q)=q^2-39,5q-20$
$\Delta=b^2-4ac=(-39,5)^2-4\times 1\times (-20)=1640,25$
$\Delta>0$ donc il y a deux racines:
$q_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{39,5-\sqrt{1640,25}}{2}=-0,5 $ et $q_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{39,5+\sqrt{1640,25}}{2}=40$

donc $B(q)\geq 0$ pour $q\in [40;50]$.
- Tracer la représentation graphique $C_R$ de la fonction $R$ dans le même repère que la fonction coût de fabrication.
Comment peut-on retrouver graphiquement le résultat de la fonction précédente?$R$ est une fonction linéaire donc sa représentation graphique est une droite passant par l'origine du repère.
Pour que le bénéfice soit positif, il faut que $R(q)$ soit supérieur à $C(q)$.$R$ est une fonction linéaire donc sa représentation graphique est une droite passant par l'origine du repère.
$R(0)=0$ et $R(50)=10,5\times 50=525$
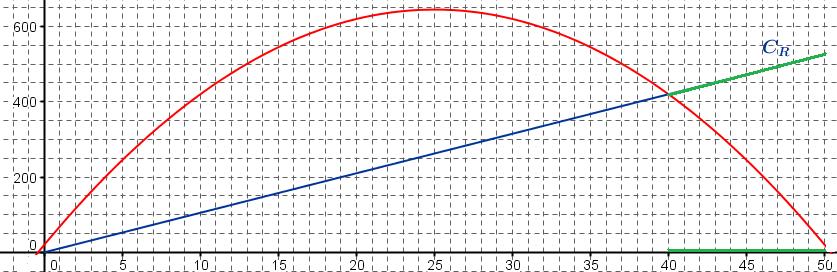
Pour que le bénéfice soit positif, il faut que $R(q)$ soit supérieur à $C(q)$ donc que la courbe $C_R$ soit au-dessus de la courbe représentant le coût total.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
