Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
On donne $P(x)=2x^3-9x^2+7x+6$ défini sur $\mathbb{R}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
- Déterminer un entier $\alpha$ racine de $P$.
On cherche donc $\alpha$ tel que $P(\alpha)=0$
On peut tester les entiers consécutifs $1$ puis 2...$P(2)=2\times 2^3-9\times 2^2+7\times 2+6=16-36+14+6=0$
Si $2$ est une racine de $P$ alors $P(2)=0$ et donc si l'on écrit $P$ sous forme d'un produit de facteurs, l'un des facteurs sera $x-2$ puisque $P$ s'annule pour $x=2$ - En développant $P(x)=(x-\alpha)(ax^2+bx+c)$ , déterminer les réels $a$, $b$ et $c$ par identification des coefficients.
On développe $(x-2)(ax^2+bx+c)$ en fonction de $a$, $b$ et $c$
On identifie les coefficients pour obtenir $2x^3-9x^2+7x+6$, autrement dit les coefficients de $x^3$ doivent être égaux, de même pour les coefficient de $x^2$...$(x-2)(ax^2+bx+c)=ax^3+bx^2+cx-2ax^2-2bx-2c$
$\phantom{(x-2)(ax^2+bx+c)}=ax^3+bx^2-2ax^2+cx-2bx-2c$
Pour tout réel $x$, on a donc $P(x)=2x^3-9x^2+7x+6=ax^3+bx^2-2ax^2+cx-2bx-2c$
Par identification des coefficients, on a:
Dans chacune des expressions le coefficient de $x^3$ vaut $2$ et $a$
donc $a=2$
Dans chacune des expressions le coefficient de $x^2$ vaut $-9$ et $b-2a$
donc $b-2a=-9 \Longleftrightarrow b-4=-9 \Longleftrightarrow b=-5$
$c-2b=7\Longleftrightarrow c+10=7 \Longleftrightarrow c=-3$
On vérifie que $-2c$ est bien égal à $-6$
$c=-3$ donc $-2c=-2\times (-3)=6$
On a donc $a=2$, $b=-5$ et $c=-3$
- En déduire les solutions de l'équation $P(x)=0$
include122fclueChaque facteur doit être égal à $0$$P(x)=(x-2)(2x^2-5x-3)$
$P(x)=0 \Longleftrightarrow (x-2)(2x^2-5x-3)=0$
$\phantom{P(x)=0} \Longleftrightarrow x-2=0$ ou $2x^2-5x-3=0$
$\phantom{P(x)=0} \Longleftrightarrow x=2$ ou $2x^2-5x-3=0$
Résolution de $2x^2-5x-3=0$
$\Delta=(-5)^2-4\times 2\times (-3)=25+24=49$
$\Delta >0$ donc il y a deux solutions:
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-7}{4}=\dfrac{-1}{2}$
$x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+7}{4}=3$
donc $P(x)=0$ pour $x=2$, $x=\dfrac{-1}{2}$ et $x=3$
$2x^2-5x-3=2(x-3)\left(x+\dfrac{1}{2}\right)$
donc peut écrire $P(x)=2(x-2)(x-3)\left(x+\dfrac{1}{2}\right)$ - Complément: division de polynômes (voir vidéo)
On peut poser la division $2x^3-9x^2+7x+6$ par $x-2$
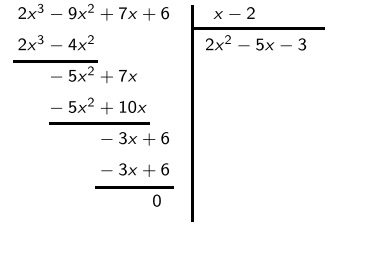
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
