Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
- Placer le point $A$ sur le cercle trigonométrique correspondant au réel $\dfrac{25\pi}{6}$ et donner la valeur exacte de $cos\left(\dfrac{25\pi}{6}\right)$ et $sin\left(\dfrac{25\pi}{6}\right)$.
Cosinus et sinus d'un nombre réel
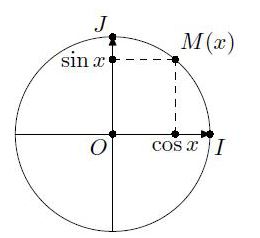
Soit $(O;I,J)$ un repère orthonormé et $\mathcal{C}$ le cercle trigonométrique. Soit $x$ un réel et $M$ le point correspondant sur le cercle.
On appelle cosinus de $x$ et on note $cos(x)$ l'abscisse du point $M$.
On appelle sinus de $x$ et on note $sin(x)$ l'ordonnée du point $M$.
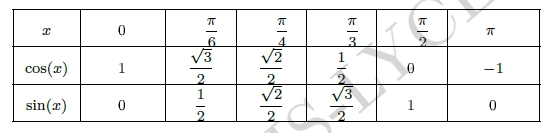
Valeurs remarquables du cos et du sin
 $2\pi=\dfrac{12\pi}{6}$
$2\pi=\dfrac{12\pi}{6}$
Il faut déterminer la mesure principale de $\dfrac{25\pi}{6}$$2\pi=\dfrac{12\pi}{6}$
$\dfrac{25}{6}\approx 4,17$
L'entier pair le plus proche du quotient $\dfrac{25}{6}$ est $k=4$
$\dfrac{25\pi}{6}-4\pi=\dfrac{25\pi}{6}-\dfrac{24\pi}{6}=\dfrac{\pi}{6}$
donc $\dfrac{25\pi}{6}=\dfrac{\pi}{6}+4\pi$ ($4\pi=2\times 2\pi$ soit deux tours)
La mesure principale de $\dfrac{25\pi}{6}$ est $\dfrac{\pi}{6}$.
2. Un autre méthode pour déterminer la mesure principale est d'écrire directement:
$\dfrac{25\pi}{6}=\dfrac{\pi}{6}+\dfrac{24\pi}{6}=\dfrac{\pi}{6}+4\pi=\dfrac{\pi}{6}+2\times 2\pi$
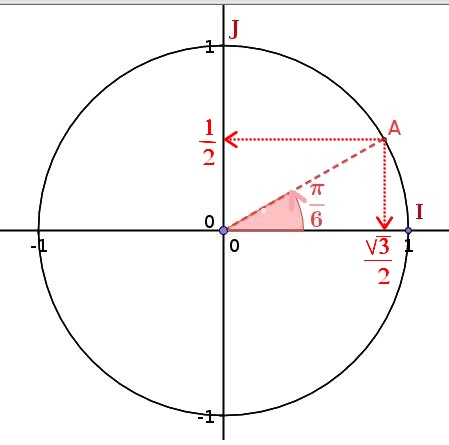
$cos\left(\dfrac{25\pi}{6}\right)=cos\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}$
et $sin\left(\dfrac{25\pi}{6}\right)=sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}$
- Placer le point $BA$ sur le cercle trigonométrique correspondant au réel $$\dfrac{-47\pi}{4}$$ et donner la valeur exacte de $cos\left(\dfrac{-47\pi}{4}\right)$ et $sin\left(\dfrac{-47\pi}{4}\right)$.
$2\pi=\dfrac{8\pi}{4}$
On peut chercher le nombre de tours entiers contenus dans $\dfrac{47\pi}{4}$ en cherchant l'arrondi au nombre entier pair le plus proche du quotient $47 \div 4$$47\div 4 = 11,75$
L'entier pair le plus proche de 11,75 est 12
$\dfrac{-47\pi}{4}+12\pi=\dfrac{-47\pi}{4}+\dfrac{48\pi}{4}$
$~~~~~~~~~~~~=\dfrac{\pi}{4}$
donc $\dfrac{-47\pi}{4}=\dfrac{\pi}{4}-12\pi$
$12\pi=6\times 2\pi$ correspond à six tours sur le cercle
On a donc $\dfrac{-47\pi}{4}=\dfrac{\pi}{4}+6\times 2\pi$
La mesure principale de $\dfrac{-47\pi}{4}$ est $\dfrac{\pi}{4}$.
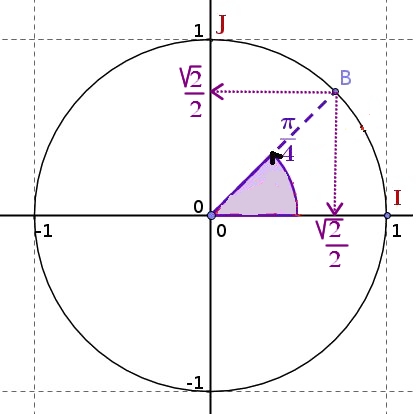
$cos\left(\dfrac{-47\pi}{4}\right)=cos\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$
et $sin\left(\dfrac{-47\pi}{4}\right)=sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
