Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
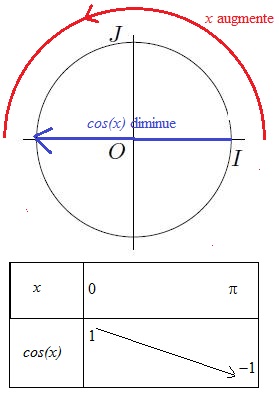
- Rappeler les propriétés de la fonction cosinus.
- Rappeler les variation de la fonction $cos$ sur $[0;\pi]$.
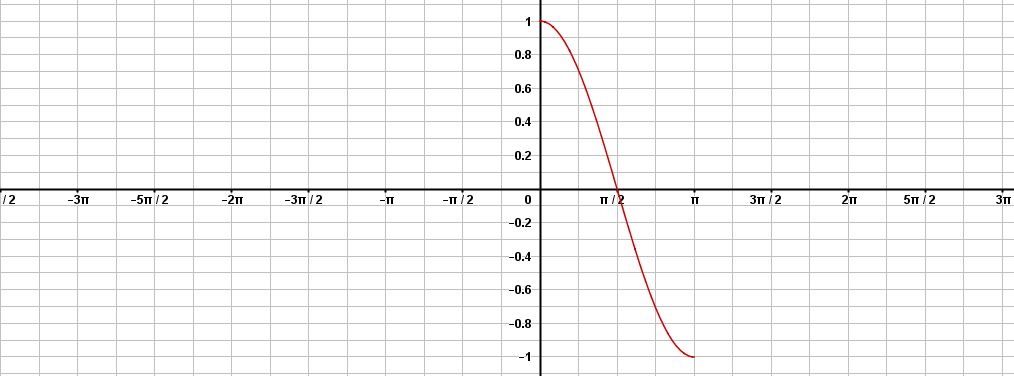
- On donne le tracé de la représentation graphique de $cos$ sur $[0;\pi[$.
Compléter le tracé de la courbe ci-dessous.
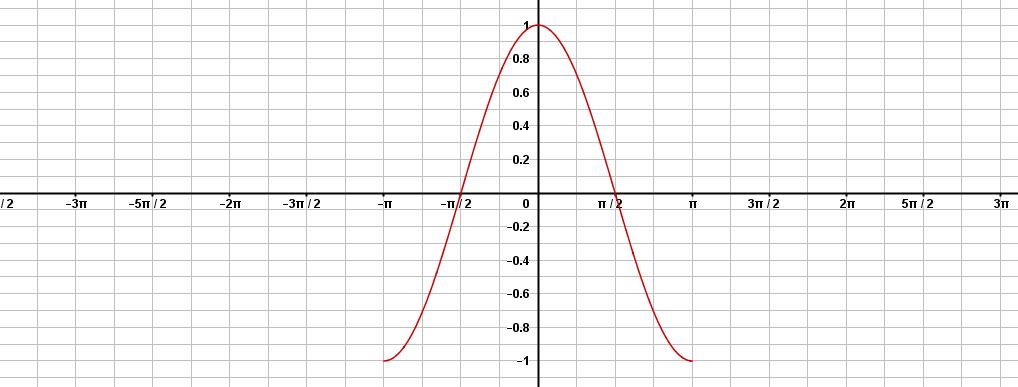
 La fonction est paire donc il y a une symétrie par rapport à l'axe des ordonnées
La fonction est paire donc il y a une symétrie par rapport à l'axe des ordonnées
$cos(x)=cos(x+2\pi)$$cos$ est paire donc sa courbe est symétrique par rapport à l'axe des ordonnées
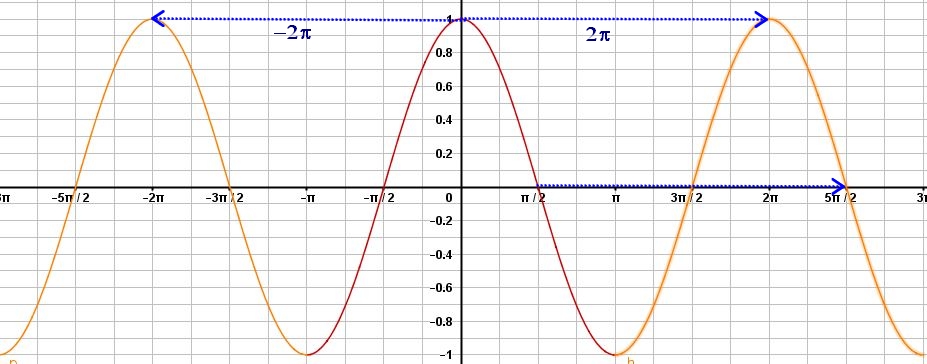
$cos$ est périodique de période $2\pi$ donc il suffit d'effectuer des translations de vecteurs $(k2\pi;0)$ avec $k\in \mathbb{Z}$.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.