Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
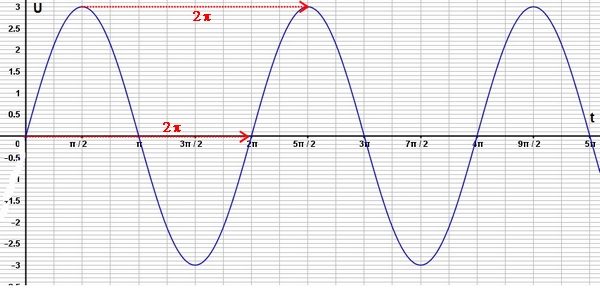
La courbe ci-dessous représente la tension en volts en fonction du temps en secondes.
On note $t$ le temps en seconde et $U$ la tension en Volts et $f$ la fonction associent $U$ à $t$.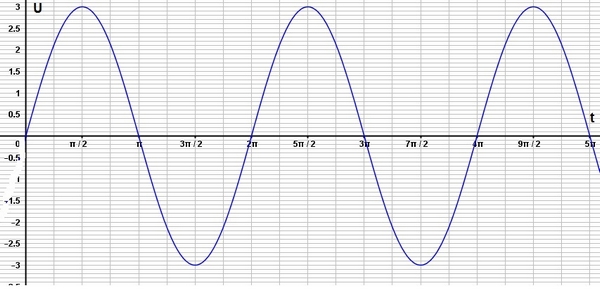
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
On note $t$ le temps en seconde et $U$ la tension en Volts et $f$ la fonction associent $U$ à $t$.

- Quelle est la période de cette tension?
La fréquence $F$ en Hertz est donnée par $F=\dfrac{1}{T}$.
Calculer $F$ en arrondissant aux centièmes. - En général on donne la tension efficace du signal notée $U_{eff}$ et on a $U_{eff}=\dfrac{U_{max}}{\sqrt{2}}$.
Sur le graphique $U_{max}=3$V.
donc $U_{eff}=\dfrac{U_{mx}}{\sqrt{2}}=\dfrac{3}{\sqrt{2}}\approx 2,12$ volts.
- On a $f(t)=3sin(t)$.
Déterminer graphiquement à quels instants on a $U=2$volts.
Avec la calculatrice, donner ces instants arrondis aux centièmes.il y a une infinité de valeurs donnant le même cosinusGraphiquement, on a $t_0\approx 0,8$ et $t_1\approx 2,4$ secondes (voir figure ci-dessous)
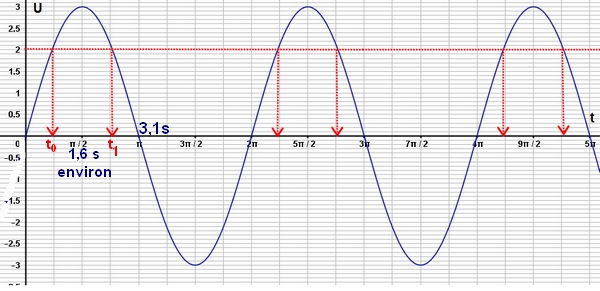
La fonction est périodique de période $2\pi$ donc on a $U=2$V pour $t=t_0+k2\pi$ puisque $f(t)=f(t+2\pi)$ ou $t=t_1+k2\pi$.
$3sin(t)=2 \Longleftrightarrow sin(t)=\dfrac{2}{3}$
Avec la calculatrice, on utilise $sin^{-1}$ (ou arcsin)
On a alors $t_0\approx 0,73$ et $t_1\approx 0,73+\pi$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.