Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
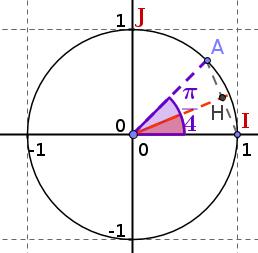
Le point $A$ est un point du cercle trigonométrique associé au réel $\dfrac{\pi}{4}$ et $H$ est le pied la hauteur issue de A dans le triangle $IOA$.(voir figure)
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)

- Calculer les coordonnées du point $A$ puis la distance $IA$.
Trigonométrie dans le triangle rectangle
$ABC$ est un triangle rectangle en $A$.
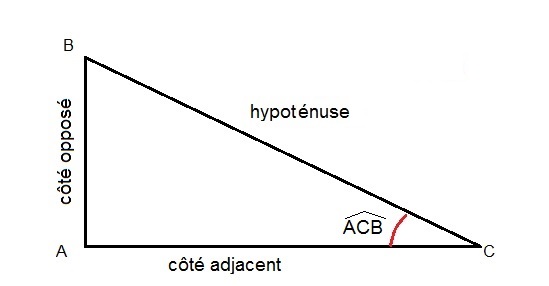
$cos(\widehat{ACB})=\dfrac{AC}{BC}=\dfrac{\text{côté adjacent}}{\text{hypoténuse}}$
$sin(\widehat{ACB})=\dfrac{AB}{BC}=\dfrac{\text{côté opposé}}{\text{hypoténuse}}$
$tan(\widehat{ACB})=\dfrac{AB}{AC}=\dfrac{\text{côté opposé}}{\text{côté adjacent}}$
Distance dans un repère
Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$On a $( \overrightarrow{OI}, \overrightarrow{OA})=\dfrac{\pi}{4}$
donc $x_A=cos(\dfrac{\pi}{4})=\dfrac{\sqrt{2}}{2}$
et $y_A=sin(\dfrac{\pi}{4})=\dfrac{\sqrt{2}}{2}$
Le repère $(O; \overrightarrow{OI}; \overrightarrow{OJ})$ est orthonormé.
$IA=\sqrt{(x_A-x_I)^2+(y_A-y_I)^2}$
$\phantom{IA}=\sqrt{\left(\dfrac{\sqrt{2}}{2}-1 \right)^2+\left(\dfrac{\sqrt{2}}{2}-0 \right)^2}$
$\phantom{IA}=\sqrt{\dfrac{2}{4}-2\dfrac{\sqrt{2}}{2}+1+\dfrac{2}{4}}$
$\phantom{IA}=\sqrt{\dfrac{1}{2}-\sqrt{2}+1+\dfrac{1}{2}}$
$\phantom{IA}=\sqrt{2-\sqrt{2}}$
- Déterminer les coordonnées de $H$ et en déduire la valeur exacte de $cos(\dfrac{\pi}{8})$ et de $sin(\dfrac{\pi}{8})$
Le triangle OIA est isocèle en O donc la hauteur issue de O est confondue avec la bissectrice de l'angle $\widehat{IOA}$
Le triangle IOH est un triangle rectangle en H.Le triangle $OIA$ est isocèle en $O$ donc la hauteur issue de $O$ est confondue avec la bissectrice de l'angle $\widehat{IOA}$
donc $( \overrightarrow{OI}; \overrightarrow{OH})=\dfrac{\dfrac{\pi}{4}}{2}=\dfrac{\pi}{8}$
Le triangle OHI est un triangle rectangle en H et on a $OI=1$
On a donc dans ce triangle(voir figure ci-dessous):
$cos(\dfrac{\pi}{8})=\dfrac{OH}{OI}=OH$
et $sin(\dfrac{\pi}{8})=\dfrac{IH}{OI}=IH$
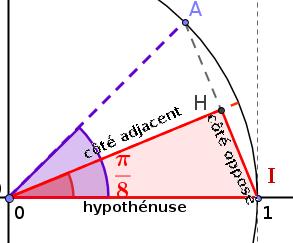
Le triangle OIA est isocèle en O donc la hauteur issue de O est confondue avec la médiane issue de O et donc H est le milieu de [IA].
$IH=\dfrac{IA}{2}=\dfrac{\sqrt{2-\sqrt{2}}}{2}$
et dans le triangle OIH rectangle en H, on a:
$IH^2+OH^2=OI^2$
$\Longleftrightarrow OH^2=1-IH^2$ (car $OI=1$)
donc $OH^2=1-\left( \dfrac{\sqrt{2-\sqrt{2}}}{2}\right)^2=1-\dfrac{2-\sqrt{2}}{4}=\dfrac{4-2+\sqrt{2}}{4}=\dfrac{2+\sqrt{2}}{4}$
Il y a le signe $-$ devant la barre de fraction soit $-\dfrac{2-\sqrt{2}}{4}=\dfrac{-2+\sqrt{2}}{4}$
donc $OH=\sqrt{\dfrac{2+\sqrt{2}}{4}}=\dfrac{\sqrt{2+\sqrt{2}}}{2}$
Vérifier les valeurs obtenues à la calculatrice. (attention au réglage des unités pour les angles) - En déduire $cos(\dfrac{3\pi}{8})$
Angles associés
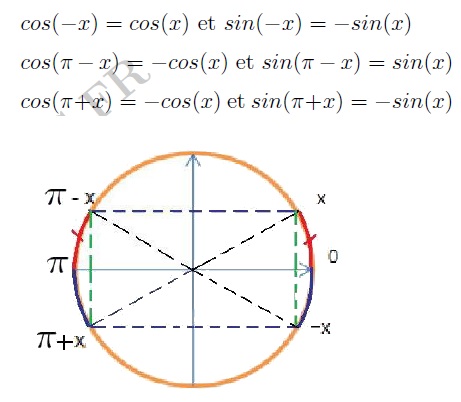 $\dfrac{\pi}{2}-\dfrac{\pi}{8}=\dfrac{3\pi}{8}$$\dfrac{\pi}{2}-\dfrac{\pi}{8}=\dfrac{3\pi}{8}$
$\dfrac{\pi}{2}-\dfrac{\pi}{8}=\dfrac{3\pi}{8}$$\dfrac{\pi}{2}-\dfrac{\pi}{8}=\dfrac{3\pi}{8}$
$cos(\dfrac{3\pi}{8})=cos(\dfrac{\pi}{2}-\dfrac{\pi}{8})=sin(\dfrac{\pi}{8})=\dfrac{\sqrt{2-\sqrt{2}}}{2}$
Penser à contrôler le résultat obtenu avec la calculatrice en calculant $cos(\dfrac{\pi}{8})$ et $\dfrac{\sqrt{2-\sqrt{2}}}{2}$
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
