Aide en ligne avec WhatsApp*, un professeur est à vos côtés à tout moment! Essayez!
Un cours particulier à la demande!
Envoyez un message WhatsApp au 07 67 45 85 81 en précisant votre nom d'utilisateur.*période d'essai ou abonnés premium(aide illimitée, accès aux PDF et suppression de la pub)
Un manège tourne à la vitesse angulaire de $\dfrac{\pi}{12}$ radians par seconde dans le sens direct.
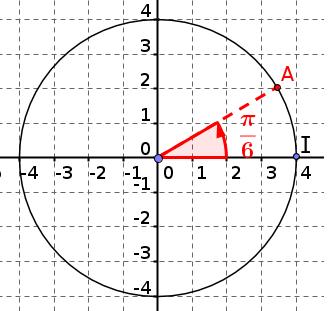
Le petit cheval de bois correspondant au point A est au départ dans la position indiquée sur le figure ci-dessous, une unité représentant 1 mètre.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
Le petit cheval de bois correspondant au point A est au départ dans la position indiquée sur le figure ci-dessous, une unité représentant 1 mètre.

- Le manège tourne pendant 3 minutes et s'arrête à nouveau.
Calculer la distance parcourue (arrondie au cm près) par ce petit cheval (point A) en mètres puis la position du point A lorsque le manège s'arrête.Si A et B sont deux points d'un cercle de centre O et de rayon $r$, la longueur de l'arc de cercle AB est $AB=\alpha \times r$ où $\alpha$ est la mesure en radians de l'angle $\widehat{AOB}$
Il faut déterminer la mesure principale correspondant au point B tel que $(\overrightarrow{OA};\overrightarrow{OB})=\alpha$ où $\alpha$ est la mesure en radians correspondant aux 3 minutes de rotation du manège au rythme de $\dfrac{\pi}{12}$ radians par seconde3 minutes=$3\times 60=180$ secondes.
ce qui correspond à une rotation de $180\times \dfrac{\pi}{12}=15\pi$ radians.
Le point A est situé à 4 mètres du centre du cercle
donc la distance parcourue par le point A est donc:
$15\pi\times 4=60\pi \approx 188,49556$
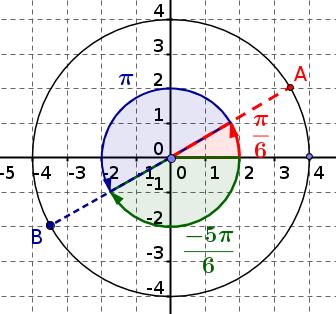
Si on note B la position du cheval de bois lorsque le manège s'arrête, on a alors:
$(\overrightarrow{OA};\overrightarrow{OB})=15\pi$
donc $(\overrightarrow{OI};\overrightarrow{OB})=(\overrightarrow{OI};\overrightarrow{OA})+(\overrightarrow{OA};\overrightarrow{OB})=\dfrac{\pi}{6}+15\pi$
donc $(\overrightarrow{OI};\overrightarrow{OB})=\dfrac{\pi}{6}+15\pi=\dfrac{\pi}{6}+\pi+14\pi$
$14\pi=7\times 2\pi$ et $2\pi$ correspond à un tour complet
donc Le point B est tel que $(\overrightarrow{OI};\overrightarrow{OB})=\dfrac{\pi}{6}+\pi=\dfrac{7\pi}{6}$
La mesure principale de cet angle est donc $\dfrac{7\pi}{6}-2\pi=\dfrac{-5\pi}{6}$
- Déterminer un temps de fonctionnement du manège permettant au cheval de bois de s'arrêter au point I de coordonnées (1;0).
Pour que le manège s'arrête en I, il faut que $(\overrightarrow{OA};\overightarrow{OB})=k2\pi-\dfrac{\pi}{6}$ avec $k\in\mathbb{Z}$Si on note B le point sur le cercle correspondant à la position du cheval de bois lorsque le manège s'arrête, pour que le manège s'arrête en I, il faut que: $(\overrightarrow{OA};\overrightarrow{OB})=(\overrightarrow{OA};\overrightarrow{OI})=-\dfrac{\pi}{6}+k2\pi$ avec $k\in\mathbb{Z}$
donc si on note $t$ le temps de fonctionnement du manège en secondes, on a alors:
$(\overrightarrow{OA};\overrightarrow{OB})=-\dfrac{\pi}{6}+k2\pi=t\times \dfrac{\pi}{12}$ avec $k\in\mathbb{Z}$
$ -\dfrac{\pi}{6}+k2\pi=t\times \dfrac{\pi}{12}$ avec $k\in\mathbb{Z}$
$\Longleftrightarrow \dfrac{-\dfrac{\pi}{6}+k2\pi}{\dfrac{\pi}{12}}=t$ avec $k\in\mathbb{Z}$
$\Longleftrightarrow (-\dfrac{\pi}{6}+k2\pi)\times \dfrac{12}{\pi}=t$ avec $k\in\mathbb{Z}$
$\Longleftrightarrow -\dfrac{12\pi}{6\pi}+\dfrac{12\times k2 \pi}{\pi}=t$ avec $k\in\mathbb{Z}$
$\Longleftrightarrow -2+24k=t$ avec $k\in\mathbb{Z}$
donc le temps $t$ de fonctionnement du manège doit être de $t=24k-2$ secondes avec $k$ entier naturel supérieur ou égal à 1.
Par exemple si $k=10$, on a $t=240-2=238$ secondes.
On a alors $(\overrightarrow{OA};\overrightarrow{OB})=238\times \dfrac{\pi}{12}=\dfrac{119\pi}{12}$
et donc $(\overrightarrow{OI};\overrightarrow{OB})= (\overrightarrow{OI};\overrightarrow{OA}) +(\overrightarrow{OA};\overrightarrow{OB})=\dfrac{\pi}{6}+\dfrac{119\pi}{6}=\dfrac{120\pi}{6}=20\pi=0+10\times 2\pi$
La mesure principale de $(\overrightarrow{OI};\overrightarrow{OB})$ est 0.
Attention les fonctions ci-dessus sont désactivées en mode "visiteur", créez un compte MATHS-LYCEE.FR (gratuit)
vidéos semblables
Pour compléter cet exercice, nous vous conseillons les vidéos suivantes semblables à l'exercice affiché.
exercices semblables
Si vous souhaitez vous entraîner un peu plus, nous vous conseillons ces exercices.
